把MIT-scheme当作计算器使用
1.每个表达式d都由()圈住,当跳出最外层()时,会在前端输出值。
2.表达式之间可以嵌套,表达式形如(操作符 参数 参数 ...),而这种表达式也被称为S-表达式
3.每个操作符实际是个函数,既然MIT-scheme可以当作计算器使用,那么它也支持基本四大运算符,加、减、乘、除,分别对应+、-、*、/
4.练习
练习 1
使用Scheme解释器计算下列式子:
1.(1+39) * (53-45)
2.(1020 / 39) + (45 * 2)
3.求和:39, 48, 72, 23, 91
4.求平均值:39, 48, 72, 23, 91(结果取为浮点数)
解答:
1.(* (+ 1 39) (+ 53 45))
2.(+ (/ 1020 39) (* 45 2))
3.(+ 39 48 72 23 91)
4.(exact->inexact (/ (+ 39 48 72 23 91) 5)) exact->inexact 分数->浮点数
5.指数函数exp和对数函数log
两者的底数都是e,只不过目前我不知道如何在scheme中表示e
6.expt,用来计算x的y次幂
例如 (expt 4 1/2),代表4的开平方
数据结构
练习1
使用cons来构建在前端表现为如下形式的数据结构。
1.("hi" . "everybody") (cons "hi" "everybody")
2.(0) (cons 0 '())
3.(1 10 . 100)
4.(1 10 100) (cons 1 (cons 10 100))
5.(#\I "saw" 3 "girls") (cons #\I (cons "saw" (cons 3 (cons "girls" '()))))
6.("Sum of" (1 2 3 4) "is" 10) (cons "Sum of" (cons (cons 1 (cons 2 (cons 3 (cons 4 '())))) (cons "is" (cons 10 '()))))
1.cons单元
cons单元由两部分构成,car和cdr,结构如下图:
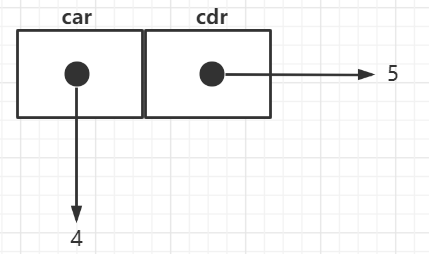
也就是说一个cons单元由两个内存单元,并且这两个内存单元存的均是地址,指向真实值的地址,所以cons单元可以理解为两个指针car、cdr组成的数据结构
通常用cons构造cons单元,形如(cons 1 2) => (1 . 2)
由于car,和cdr存的是指针,因而它们可以指向任意类型的值
另外(cons 1 2)表达式构造了一个cons单元,而cons单元实际是一块内存,因而它的返回值是一个地址,这也代表cons单元可以互相嵌套或者说进行串联
2.表
表是Cons单元通过用cdr部分连接到下一个Cons单元的开头实现的。这个定义显然具有递归性,即表(cons 1 表),用图表示如下:
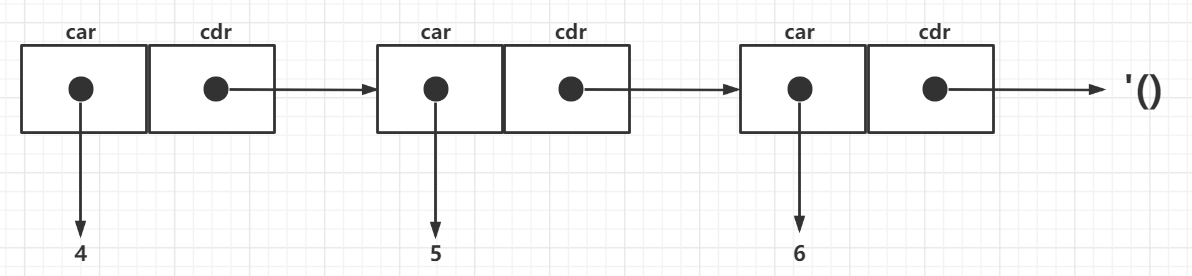
其中'()表示空表,就算数据仅由一个Cons单元组成,只要它的cdr单元是’(),那它就是一个表。在练习1中2、4、5、6均是表结构
3.原子
不使用Cons单元的数据结构称为原子(atom)。数字,字符,字符串,向量和空表’()都是原子。’()既是原子,又是表。
4.引用
所有的记号都会依据Scheme的求值规则求值:所有记号都会从最内层的括号依次向外层括号求值,且最外层括号返回的值将作为S-表达式的值。而引用能够阻止记号被求值,形如(quote (+ 1 2)),将会返回(+ 1 2),而不是3,而quote一般简写为 ',(quote (+ 1 2)) == ‘(+ 1 2)。**实际上MIT-Scheme用()表示空表,不过在程序中表示空表应该用'(),显然'(1, 2, 3, 4)则代表(1, 2, 3, 4)表。
5.list函数
list函数的存在使得表的构建变得简单(代码编写更简单)
如练习1中所示,(“Sum of” (1 2 3 4) “is” 10)用cons构造是这样的:(cons “Sum of” (cons (cons 1 (cons 2 (cons 3 (cons 4 ‘())))) (cons “is” (cons 10 ‘())))),但是如果用list函数,它是这样的:(list “Sum of” ‘(1 2 3 4) “is” 10)
也就是说list接收任意数量的参数,并能将其构造串联成表
6.car函数,cdr函数
见名知意,分别是获取cons单元的car部分和cdr部分,如果是串联的cons单元,car获取的是第一个cons单元的car部分,而cdr获取的是第一个cons单元的cdr部分,也就是后面的整个串联的部分
函数
1.define和set!
使用define来将一个符号与一个值绑定。可以通过这个操作符定义例如数、字符、表、函数等任何类型的全局参数。形如 (define sig value)
2.自定义函数的两种方式
- 用lambda定义过程
(define hello (lambda (name)
(string-append "hello " name "!")))
这里的调用很想Java中的lambda表达式,(args) -> {method body},只不过没有 ->,也许Java就是借鉴的scheme也说不定
- 函数的短定义形式
(define (hello name)
(string-append "hello " name "!"))
函数的短定义与函数的调用格式非常相像,并且注意函数体可以是多个S—表达式
3.define 定义全局变量
; 定义全局变量name
(define name "chezscheme")
; 定义函数
(define hello (lambda (name)
(string-append "hello " name "!")))
; 调用函数
(hello name)
4.define和set!的区别
define定义的变量只在define所在的scope中可见,一个典型例子就是:在函数中define的变量在函数外部是无法访问的
而set!定义的变量才是真正的全局变量
eq?、eqv?、equal?
都只接收两个参数,但三者有小小的区别,eq?比较地址值;eqv?适合比较数字(按照值和类型进行比较,如1+2和2+1相等,但3和3.0不同,因为类型不同);equal?适合比较表和字符串等类似的序列
and、or
| 接收任意数量的参数,但这两者不等同于C语言或Java中的&&和 | ,但却继承了它们的短路特性 |
这两个操作符都会对传入的参数挨个求值,and遇到#f返回,否则返回最后一个参数,or遇到非#f返回,否则返回最后一个参数
比较运算符=、<、>、<=、>=
这些操作符允许传入任意数量的参数,只要参数传入的顺序符合操作符的语义,则返回#t,否则返回#f
分支语句
1.if语句
形如:
(if predicate then_value else_value)
2.cond语句
Java或者C语言中的switch语句,形如:
(cond
(predicate_1 clauses_1)
(predicate_2 clauses_2)
......
(predicate_n clauses_n)
(else clauses_else))
(define (fee age)
(cond
((or (<= age 3) (>= age 65)) 0)
((<= 4 age 6) 0.5)
((<= 7 age 12) 1.0)
((<= 13 age 15) 1.5)
((<= 16 age 18) 1.8)
(else 2.0)))
在clauses中可以写任意数量的表达式,但最终会返回最后一条表达式;不知道scheme中有没有return语句,这相当于return语句只能出现在语句最后了啊!
let定义局部变量
实际上,let表达式只是lambda表达式的一个语法糖:
(let ((p1 v1) (p2 v2) ...) exp1 exp2 ...)
;⇒
((lambda (p1 p2 ...)
exp1 exp2 ...) v1 v2)
p是变量,v是给p赋的值,或者说,v绑定给p
尾递归
1.尾递归于递归
递归虽然可读性很强,但有两个明显的缺点:①占用内存(方法占用内存栈)②效率低(方法调用开销,要等待方法返回值)
而尾递归参数中用一个来存最终的结果,最终结果出来的时候就直接返回了;因此在效率上是要比普通递归要好的,实际上尾递归就是循环
命名let和letrec
命名let就是let定义有了名字,形如:
(define (fact-let n)
(let loop((n1 n) (p n)) ; 1
(if (= n1 1)
p
(let ((m (- n1 1)))
(loop m (* p m)))))) ; 2
letrec和let很相似,但letrec能将一个过程(lambda定义的)与一个参数绑定(其实就相当定义了一个函数),形如:
(define (fact-letrec n)
(letrec ((iter (lambda (n1 p)
(if (= n1 1)
p
(let ((m (- n1 1)))
(iter m (* p m))))))) ; *
(iter n n)))
(fact-letrec 1000)
流式计算
; 构建一个以整数1为起点的无穷整数流
(define (integers-from n)
(cons-stream n
(integers-from (+ n 1))))
; 流s1
(define s1 (integers-from 1))
; 流s2
(define s2 (integers-from 2))
; 获取指定索引值下的流中的元素
(define (nth-stream n s)
(if (= n 0)
(head s)
(nth-stream (- n 1) (tail s))))
; 获取索引为1000000的流的元素
(nth-stream 1000000 s1)
; map流(对流的每个元素进行处理,最后返回流)
(define (scale-stream stream factor)
(stream-map (lambda (x) (* x factor)) stream))
(nth-stream 0 (scale-stream s1 4))
; 合并流
(define (add-streams s1 s2)
(cond ((empty-stream? s1) s2)
((empty-stream? s2) s1)
(else
(cons-stream
(+ (head s1) (head s2))
(add-streams (tail s1)
(tail s2))))))
; Fibonacci 的流式计算
(define fibs
(cons-stream 0
(cons-stream 1
(add-streams (tail fibs) fibs))))
(nth-stream 4 fibs)
