首页 详解贪心算法
文章
取消

详解贪心算法

作者 flameking
发表于 2022-10-15 更新于 01-02 14 分钟阅读

介绍贪心算法

在某个标准下，优先考虑满足标准的样本，最后考虑最不满足标准的样本，最终得到一个答案的算法，叫做贪心算法（相当于基于某个标准做个排序），也就是说贪心算法不从整体最优上加以考虑，所做出的是在某种意义上的局部最优解，其中由局部最优 –> 整体最优的证明可能会很困难，也可能证明出来压根就是错误的，而对于确定的算法有时候可能又必须要求全局最优，这时候就需要局部最优 –> 整体最优的证明

贪心算法在笔试中的解题套路

  1. 实现一个不依靠贪心策略的解法 X，可以用暴力的尝试
  2. 脑补出贪心策略 A、B、C……
  3. 用解法 X，和对数器，去验证每个贪心策略，用实验的方式得知哪个贪心策略正确
  4. 不要去纠结贪心策略的证明（因为往往需要复杂的数学证明，即证明耗时长，难度大），当然常见的证明方法：举反例，这种方法是最高效的
  5. 另外贪心算法试题在笔试中占比可能比较少（因为贪心 code 很容易，重点在于能不能想到贪心策略，这就容易导致 0-1 分化的局面）

贪心策略的技巧

  1. 根据某标准建立一个比较器来排序
  2. 根据某标准建立一个比较器来组成堆

经典贪心例题-会议室

一些项目要占用一个会议室宣讲，会议室不能同时容纳两个项目的宣讲。给你每个项目开始的时间和结束的时间（给你一个数组，里面是一个个具体的项目，你来安排宣讲的日程，要求会议室进行的宣讲的场次最多。返回这个最多的宣讲次数。）

原题连接

思路：

  1. 我们的排序标准是哪个会议结束的时间早来优先安排（即按照会议结束时间进行排序）
  2. 每安排一个结束时间最早的会议就把与其冲突的会议排除，最后能安排的会议室就是最多的

code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

public static class Program{
    public int start;
    public int end;
    public Program(int start, int end){
        this.start = start;
        this.end = end;
    }
}
public static class ProgramComparator implements Comparator<Program>{
    @Override
    public int compare(Program o1, Program o2){
        return o1.end - o2.end;
    }
}
public static int bestArrange(Program[] programs, int timePoint){
    Arrays.sort(programs, new ProgramComparator());
    int result = 0;
    //按结束时间升序排好的数组
    for(int i = 0; i < programs.length; i++){
        //当前时间之后的会议能够安排
        if(timePoint <= programs[i].start){
            result++;
            //以第一个结束时间最早的会议结束时间更新当前时间
            timePoint = programs[i].end;    //排除其他于进行中的会议冲突的会议
        }
    }
    return result;
}

贪心证明-将若干字符串连接保证字典序最小

证明较为复杂，可前往 B 站左程云的相关课程观看

ab 和 abc，字典序比较 ab < abc

原题链接

贪心例题

切金条-哈夫曼编码问题

例题如下：

切金条

思路：

  1. 将给定数组的数据全部放入小根堆中
  2. 每次弹出两个数做结合（相加），然后把结合后的数字放入小根堆
  3. 重复以上操作，直到弹出两个数后，小根堆为空，最后小根堆内只有一个数据

code 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14

public static int lessMony(int[] arr){
    PriorityQueue<Integer> pQ = new PriorityQueue<>();
    for(int i = 0; i < arr.length; i++){
        pQ.add(arr[i]);
    }
    int sum = 0;
    int cur = 0;
    while(pQ.size() > 1){
        cur = pQ.poll() + pQ.poll();
        sum += cur;
        pQ.add(cur);
    }
    return sum;
}

项目起始资金和最后最大资金

例题如下：

题意：给出项目清单，每个项目由启动资金和利润两个数据构成，要求计算做完项目后（有些项目可能因为启动资金比较大，做不了）获得的最大钱数。

思路：

  1. 准备一个按照项目启动资金排序的小根堆和一个按利润排序的大根堆
  2. 根据开发者拥有的资金 X，从小根堆中弹出 <= X 的数据到大根堆
  3. 然后从大根堆中弹出一个要做的项目，更新开发者拥有的资金，每次更新就继续执行 2 步骤
  4. 重复 2，3 操作，直到大根堆为空

code 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

public class Solution{
    public static class Node{
        public int p;
        public int c;
        public Node(int p, int c){
            this.p = p;
            this.c = c;
        }
    }
    public static class MinCostComparator implements Comparator<Node>{
        @Override
        public int compare(Node o1, Node o2){
            return o1.c - o2.c;
        }
    }
    public static class MaxProfitComparator implements Comparator<Node>{
        @Override
        public int compare(Node o1, Node o2){
            return o2.p - o1.p;
        }
    }
    public static int findMaximizedCapital(int k, int W, int[] Profits, int[] Capital){
        PriorityQueue<Node> minCostQ = new PriorityQueue<>(new MinCostComparator());
        PriorityQueue<Node> maxProfitQ = new PriorityQueue<>(new MaxProfitComparator());
        // 所有项目扔到被锁池中，花费组织的小根堆
        for(int i = 0; i < Profits.length; i++){
            minCostQ.add(new Node(Profits[i], Capital[i]));
        }
        for(int i = 0; i < k; i++){ // 进行 k 轮
            // 能力所及的项目，全解锁
            while(!minCostQ.isEmpty() && minCostQ.peek.c <= W){
                maxProfitQ.add(minCostQ.poll());
            }
            if(maxProfitQ.isEmpty()){   //大根堆为空，流程结束
                return W;
            }
            W += maxProfitQ.poll().p;
        }
        return W;
    }
}

动态寻找中位数-堆的应用

在一个数据流中，随时可以取得中位数

思路：

  1. 准备一个大根堆和小根堆，对数据流中的每个数，判断是否 <= 大根堆堆顶的数据，如果是扔进大根堆，否则进小根堆
  2. 对于大根堆的 sizeA，和小根堆的 sizeB，判断是否sizeA - sizeB== 2，如果是，size 大的一方弹出堆顶的数据到另一个堆
  3. 重复 1、2 操作直到数据流结束，如果数据流的总数是偶数，中位数就是大小根堆堆顶数据的和 / 2，否则就是 size 较大方的堆顶数据

其实 1、2 的操作达到的效果就是将n个数据，较小的 n / 2，和较大的 n / 2 分别保存在两个堆中

N 皇后问题

例题如下：

N 皇后问题

题意：给定一个 n * n 的棋盘，要求摆放 n 个棋子，并且所有棋子不同列不同行不在同一斜线，求共有几种摆法。

思路：

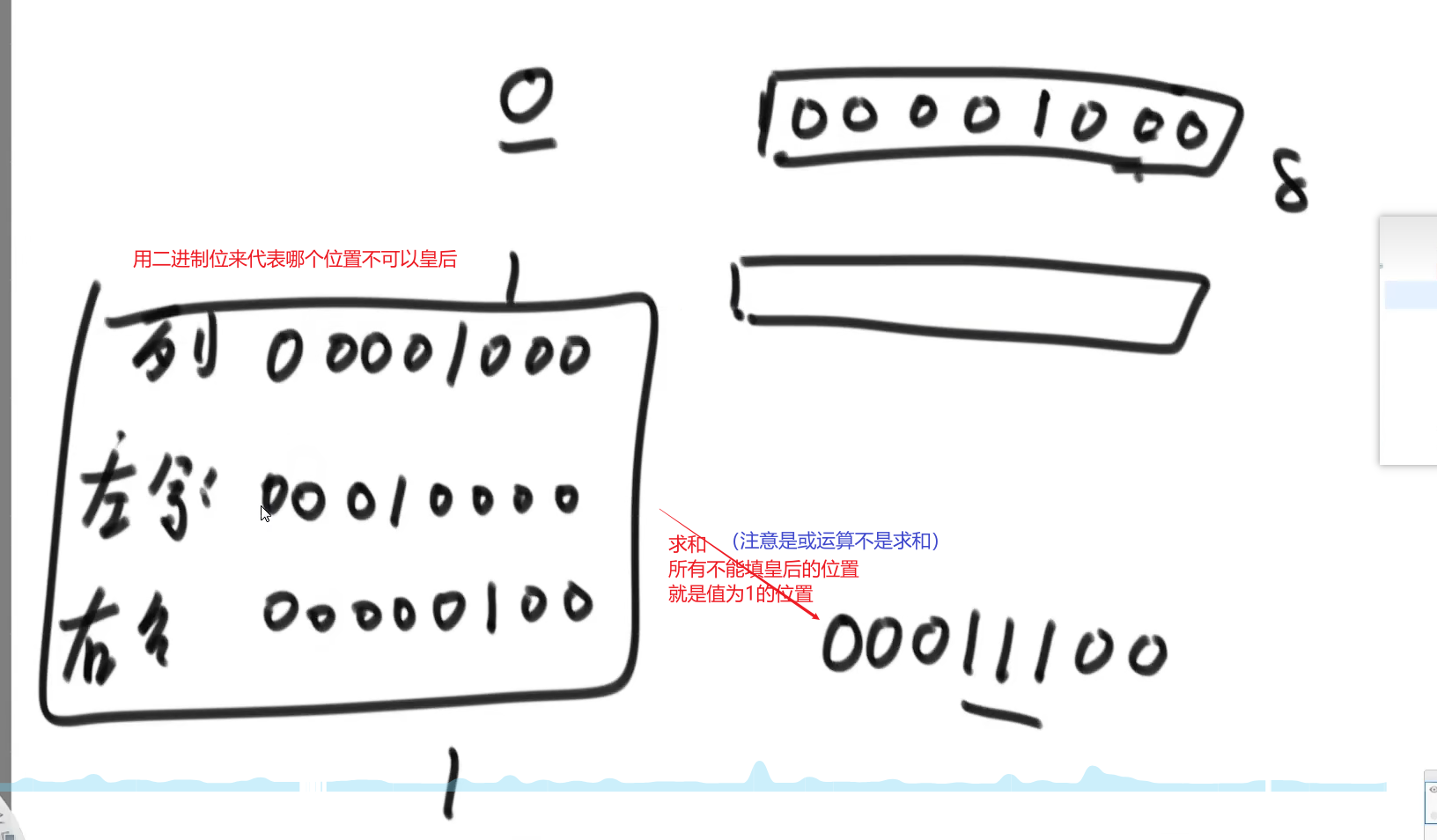
第一种：依然是深度优先遍历，通过暴力尝试，根据要求走出一条合适的摆法 第二种：位运算优化，棋盘是 n * n 形式的，那么就用一个 n 位的二进制数表示棋盘中的一行，改行某个位置能不能放棋盘由二进制位的值（0-1）决定，而这个二进制数随着棋子的摆放会不断更新，总之改二进制数就表示了能摆放棋子的位置。

code 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

public class Solution{
    public static int num1(int n){
        if(n < 1){  //n < 1 不合法，默认返回 0
            return 0;
        }
        int[] record = new int[n];  //record[i]：i行的皇后放在了第几列
        return process1(0, record, n);
    }
    /**
     * 潜台词：record[0...i-1]各行已经放了皇后，并且任何两个皇后一定都不共行、不共列、不共斜线
     * 目前来到第 i 行
     * n 代表一共有 n 行
     * 返回值是：摆完所有的皇后合理的摆法有多少种
     */
    public static int process1(int i, int[] record, int n){
        if(i == n){ //终止行
            return 1;
        }
        int res = 0;
        for(int j = 0; j < n; j++){ //在 i 行尝试所有的列
            if(isValid(record, i, j)){  //第 i 行的皇后放在 j 列，并且不与 0~i-1 的皇后共行共列共斜线
                record[i] = j;
                res += process1(i + 1, record, n);
            }
        }
        return res;
    }
    /**
     * 潜台词：当前是 i 行，因此与 0~i-1 一定不同行
     */
    public static boolean isValid(int[] record, int i, int j){
        for(int k = 0; k < i; k++){ //record[k]：0~i-1 行的皇后放的列
            if(j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)){   //同列、同斜线（行数差值 == 列数差值成45°：同斜线）不合法
                return false;
            }
        }
        return true;
    }
}

时间复杂度：n!，即一共 n 行，每行会有 n 个摆放位置的可能，所以是 n!;

常量级优化-位运算加速

思路：

优化思路

code 如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

public class Solution{
    public static int num2(int n){
        if(n < 1 || n > 32){    //int 类型最多 32 位
            return 0;
        }
        //limit 表示所有能放皇后的位置，1 能放，0 不能放
        int limit = (n == 32 ? -1 : (1 << n) - 1);
        return process2(limit, 0, 0, 0);
    }

    public static int process2(int limit, 
        int coLim, //列限制，1 的位置不能放皇后，0 的位置可以
        int leftDiaLim, //左斜线限制，1 的位置不能放皇后，0 的位置可以
        int rightDiaLim){   //右斜线限制，1 的位置不能放皇后，0 的位置可以
        if(colLim == limit){    //base case
            return 1;
        }
        //所有候选皇后的位置都在 pos 上，最终 1 的位置能放皇后，0 不能
        int pos = limit & (~(colLim | leftDiaLim | rightDiaLim));
        int mostRightOne = 0;
        int res = 0;
        while(pos != 0){ //对候选的位置（即为 1 的位置）一个一个试
            mostRightOne = pos & (~pos + 1);    //每次从最右的 1 开始
            pos = pos - mostRightOne; //将占用的位置置为 0
            res += process2(limit, 
                    colLim | mostRightOne,
                    (leftDiaLim | mostRightOne) << 1,   //左斜线限制或运算后左移
                    (rightDiaLim | mostRightOne >>> 1));    //右斜线限制或运算后右移
        }
        return res;
    }
}
算法与数据结构
本文由作者按照 CC BY 4.0 进行授权
最近更新
文章内容