二叉树

完全二叉树和满二叉树

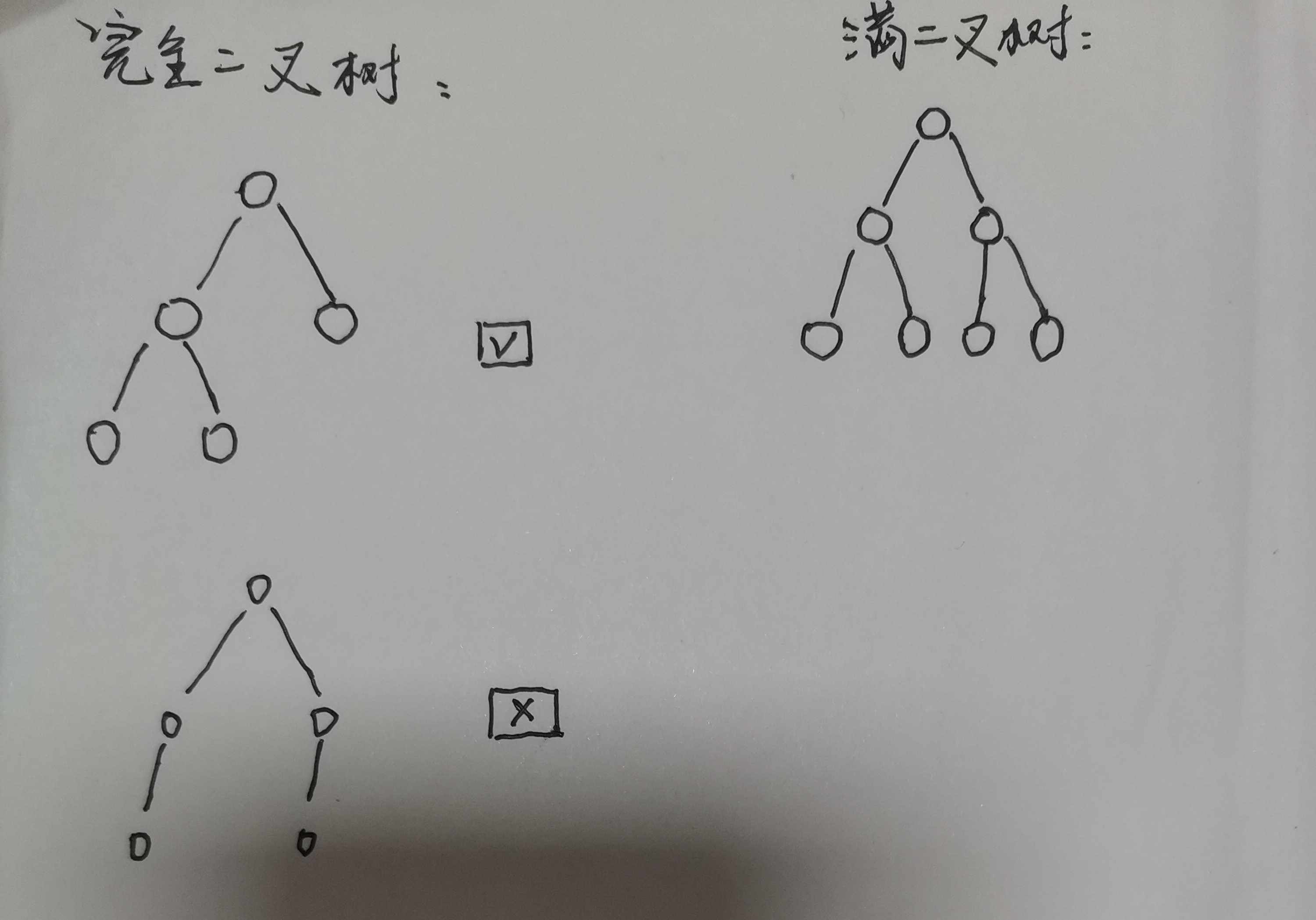
二叉树的高度

如果二叉树只有根节点，那么高度为1

数组与完全二叉树

按照数组的顺序，依次填满完全二叉树：我们发现
数组对应成二叉树

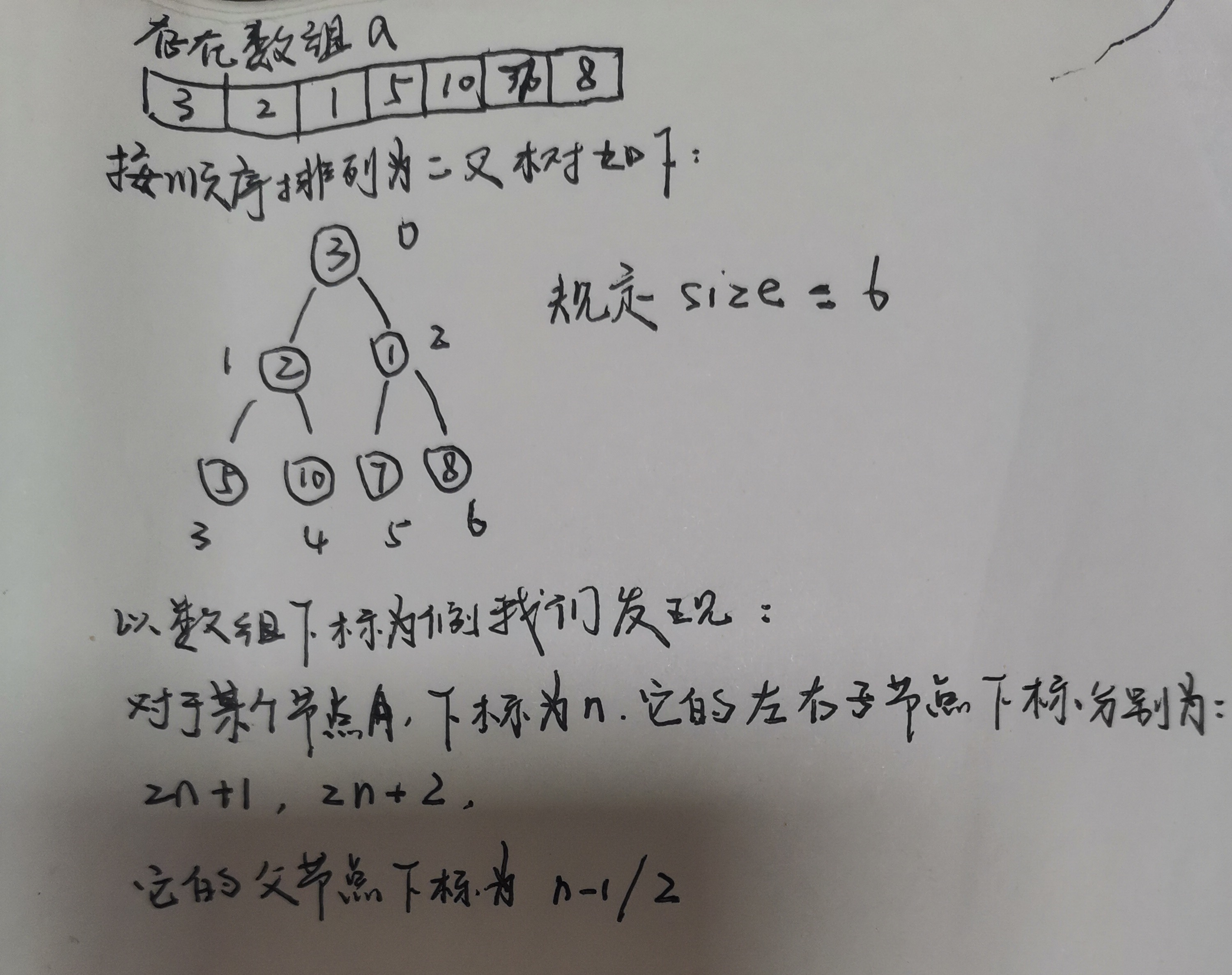
即对于节点A，下标为n，左孩子对应下标为：2n+1，右孩子对应下标为：2n+2，父节点对应下标为：n-1/2

堆、大根堆和小根堆

堆本质上就是完全二叉树，大根堆特性：对于任意根节点n都有value(n)>=value(2n+1)&&value(n)>=value(2n+2)，即对于任意父节点所有的子树节点都比它小；小根堆则相反

数组与堆

heapInsert调堆

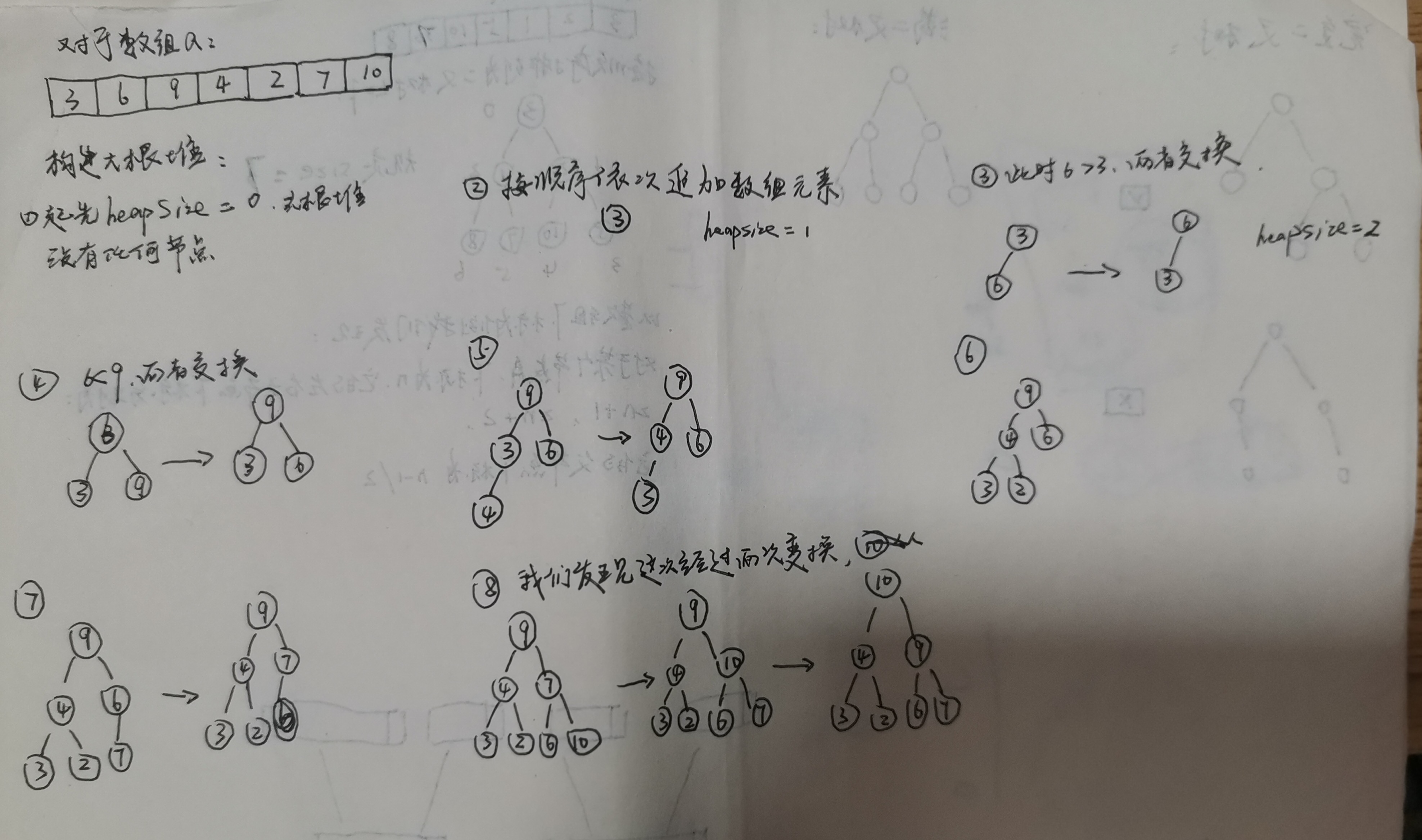
像这样大根堆起初的heapSize为0，不断追加数组中的元素，heapSize++，同时会执行heapInsert过程调正大根堆，heapInsert是由子节点不断往上替换小值的过程
直到value(n) < value((n-1/2))或n = 0

移除堆的根元素

首先如何从堆中排除根元素：

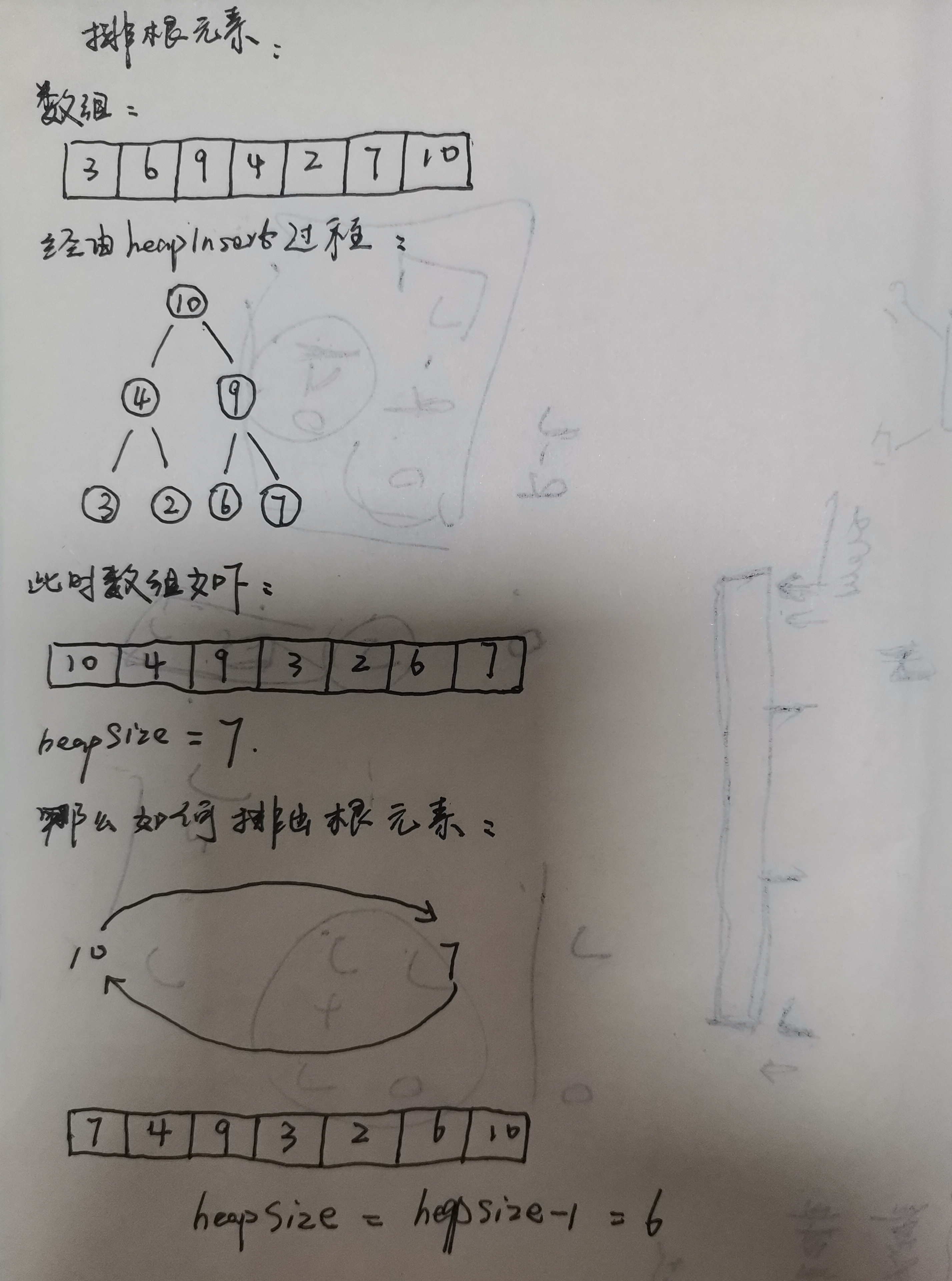
因为经过heapInsert过程，堆的首元素就是根元素，将根元素与堆末尾元素交换，然后heapSize–就排除了根元素，此时数组长度-堆长度等于1

然后heapify：
heapify过程

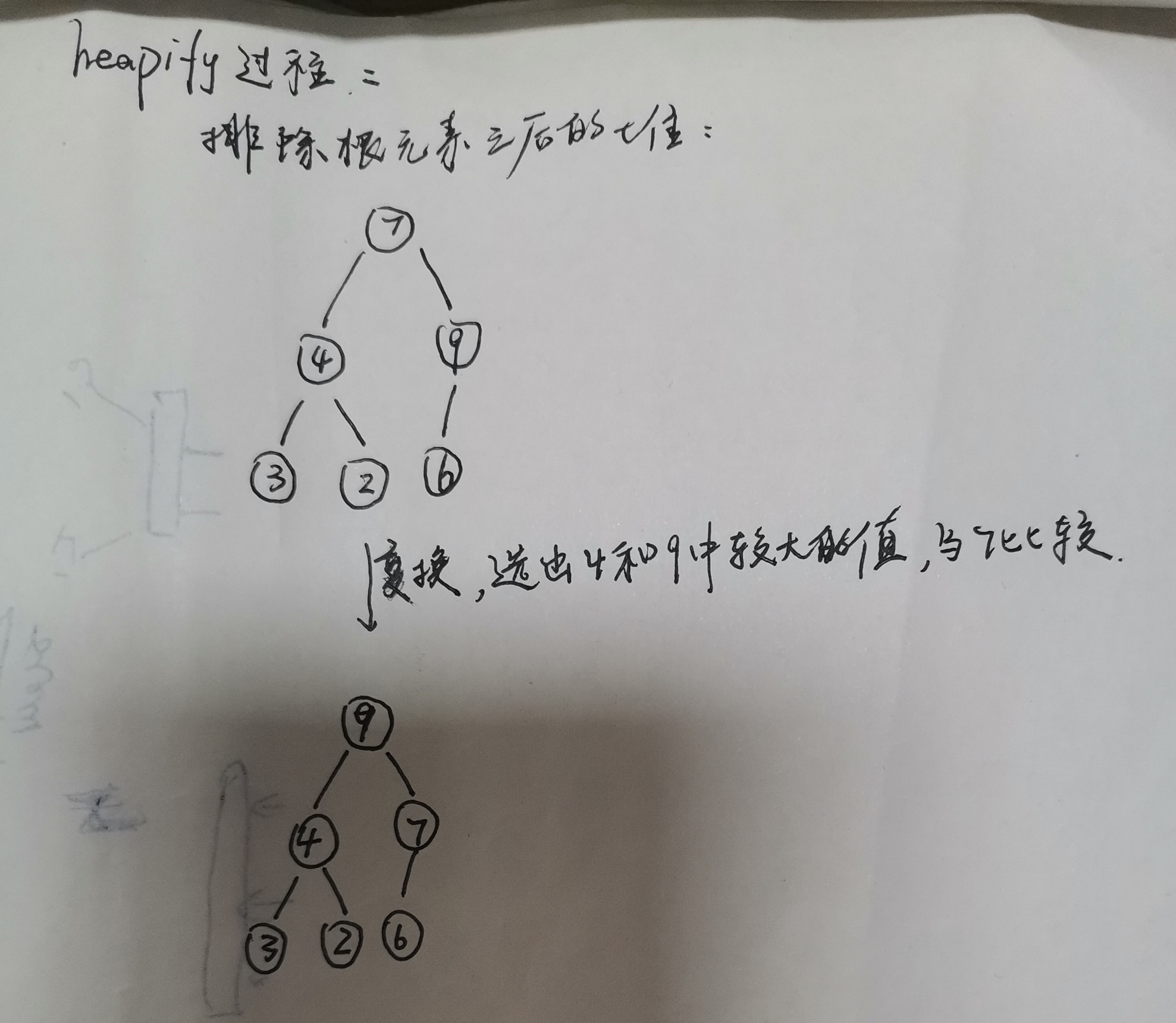
heapify过程大致如下：
父元素等于左右子树中较大者比较，如果父元素小，交换，否则不动，直到没有左右子树，即2n+1>=heapSize停止heapify过程；
我们发现heapify是一个向下的过程

替换堆的某个节点

需要先判断是应该执行heapInsert还是heapify过程，如果以该数为根节点的子树依然满足大根堆，说明不用执行heapify过程，如果该数所在的子树也满足大根堆说明也不用heapInsert过程

堆排序

  
public class HeapSort { // 大根堆排序
  public static void heapSort(int[] arr){
    if (arr == null || arr.length < 2) {
      return;
    }
//    for (int i = 0; i < arr.length; i++) {
//      heapInsert(arr, i);
//    }

    for (int i = arr.length-1; i >= 0 ; --i) { // 此时堆的长度就是数组的长度，每次heapify保证子树为大根堆，最终整个是大根堆
      heapify(arr, i, arr.length);  // 这种写法稍快
    }

    int heapSize = arr.length;
    swap(arr, 0, --heapSize);
    while (heapSize > 0){ // 堆是否为空
      heapify(arr, 0, heapSize);
      swap(arr, 0, --heapSize);
    }
  }

  private static void heapify(int[] arr, int index, int heapSize) {
    int left = index * 2 + 1;
    while(left < heapSize){
      int largest = left + 1 < heapSize && arr[left + 1] > arr[left] ?  // 在这里判断右孩子是否越界
              left + 1 : left;
      largest = arr[largest] > arr[index] ? largest : index;  // 求出父与子中较大者的下标
      if (largest == index){  // 父就是大，不再heapify
        break;
      }
      swap(arr, largest, index);
      // 重复while操作
      index = largest;
      left = index * 2 + 1;
    }

  }

  private static void heapInsert(int[] arr, int index) {
    while(arr[index] > arr[(index-1)/2]){ // index=0,条件=退出
      swap(arr, index, (index-1)/2);
      index = (index-1)/2;
    }
  }

  private static void swap(int[] arr, int a, int b) {
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
  }
}

堆排序总结

如果下标不从0开始，而是1，那么子节点下标A和父节点下标B有：A >> 1 = B
大根堆使用用于排序，小根堆不适合，如果硬要使用小根堆的话最后还要反转，（不过在heapiy阶段不交换尾部和头部的值，采取头部++的操作是不可行的，因为这样不好确认左子节点是否超出界限），所以总结来说小根堆不适合排序（适合排倒序）

优先队列与堆

优先队列与小根堆

  
public class PriorityQueueSort {
  public static void priorityQueueSort(int[] arr){
    PriorityQueue<Integer> smallHeap = new PriorityQueue<>(); // 默认小根堆，且升序
    for (int num : arr) {
      smallHeap.add(num);
    }
    for (int i = 0; i < arr.length; i++) {   // 我们发现PriorityQueue每次需要Poll输出元素，最终的数组序列才是有序的
      Integer poll = smallHeap.poll();
      System.out.print(poll + " ");
    }
  }


  public static void main(String[] args) {
    int[] arr = new int[]{38, 43 , 45, 20, 23, 100, 1, 4, 19 };
    priorityQueueSort(arr);
  }

}

理解优先队列：
1.默认情况下的优先队列其实就是小根堆，每次poll的过程其实包含：从堆中去除根元素，然后heapify，在这样反复的poll，输出的元素就是有序的，因为每次输出了小根堆的根元素
2.如果让我自己手写小根堆，思路和大根堆一样，不过最后需要排序出来后是倒叙的，所以需要首位交换元素

优先队列与大根堆

一行语句就可以设置优先队列为大根堆：PriorityQueue<Integer> queue = new PriorityQueue<>((o1, o2) -> o2 - o1);
构造函数传入的参数其实就是比较器Comparator，只不过这里使用的是lambda的写法

比较器

对于所有的比较器，返回值为-，第一个参数放前面，返回值为+，第二参数放前面，返回0，无所谓返回哪个参数，大致看下比较器的类结构：
比较器类结构

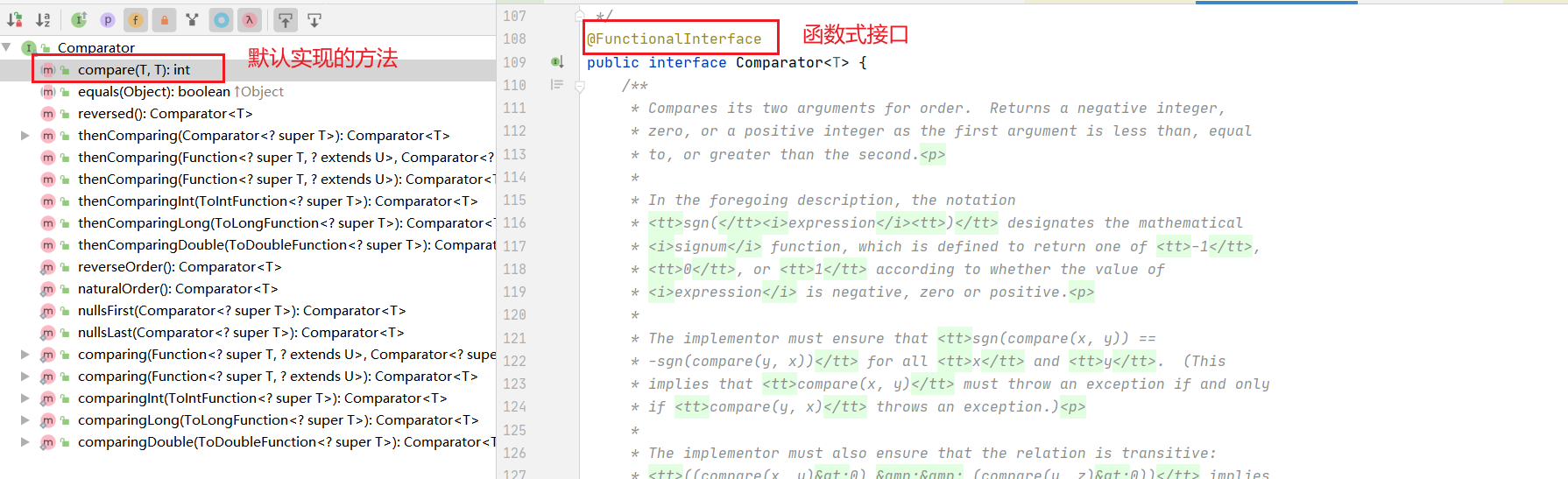
可见Comparator它是函数式接口，因此我们就可以使用lambda表达式传递Comparator对象

优先队列扩容的复杂度和影响

优先队列会如何扩容：默认数组容量不足时，会扩容成原来的2倍，也就是说原来的数组长度是10，经过第一次扩容后长度是20
如果经过多次扩容后数组的长度是N，那么数组扩容的多少次：logN次
每次扩容后原数组和当前数组不是同一个，所以会将原数组的元素拷贝进当前数组，时间复杂度是O(N)
平均到每个元素，平均时间复杂度是：NlogN/N = logN，而堆排序的时间复杂度是O(NlogN)，所以扩容是不会对排序本身的时间复杂度造成影响

手写堆的原因

虽然我们可以不手写堆，而使用PriorityQueue，但大多数情况下我们是需要手写堆的，原因：

优先队列无法修改堆中的某个元素，并重新堆化
不能直接获取堆中某个下标的值，如果要获取需先将优先队列转化成数组

常见例题

小范围排序
思路：小根堆维护k个元素，每再加入一个元素，此时的根元素一定排在数组第一个，因为数组原来的位置与排好序的位置距离不超过k
前 K 个高频元素
首先得计算每个数组元素出现得频次，然后依据频次维护小根堆，并保持size=k，每次有更大的频次就需要add，同时为了保持size=k，需要弹出根元素；该题的难点在于：如何再求出前k个高频次数字后求出其对应的元素，再我的写法中PriorityQueue维护的是Map.Emtry<Integer,Integer>，并且优先队列的比较规则是O1.getValue()-O2.getValue()，也就是小根堆；最后取出元素的时候调用O.getKey()就行了也可使用快排的局部排序法

稳定排序

稳定性的意义

这里的稳定性指的就是能够继承原来的排序次序，例如如果我原来是按照价格升序排序，现在要按找销量降序，那么如果是稳定排序，如果销量相同，次序依然会保留原来的价格排序，这样商品的次序就可以描述为最物美价廉，如果不是稳定排序，那么次序是不能保证的

排序稳定性总结：

	时	空	稳
选择	O(N^2)	O(1)	否
冒泡	O(N^2)	O(1)	是
插入	O(N^2)	O(1)	是
归并	O(NlogN)	O(N)	是
快排（随机数）	O(NlogN)	O(logN)	否
堆	O(NlogN)	O(1)	否

注意：
1.经过实验统计，快排确实最快，所以能尽量用快排就用
2.除非对空间有限制用堆排，其余尽量用快排
3.目前没有发现时间复杂度是O(logN)，空间复杂度在O(N)以下，又稳定的排序

非比较排序

像这种排序，必须通过自己分析数据状况，自己设计解法；比较排序只要给定数据比较的规则，放入数据它就会返回给你有序的数据

计数排序

常见应用场景：按年龄排序

因为年龄最大不会超过200，所以构建一个长度为200的数组，用数组下标代表年龄，数组值代表相同年龄的人的个数，遍历数组，个数*下标填充排序数组后就是正确的序列
可见计数排序会受数据的范围影响，因为我们的数组不可能建的无限大

这就是计数排序的一个常见的应用场景：词频计数

基数排序（桶排序）

基数排序的步骤：

按照数组中最大数的位数，将其与不足位数的数用0在前面补齐
准备最多10个桶（0~9）
将每个数从个位数开始一次放入对应的桶，然后按从0~9的次序一次倒出排好序，接下来换十位重复操作
最后倒出来的数据就会有序

总结：
1.因为每次进桶出桶是按照某一位进行排序的，并且每次排序的次序被继承下来了，最后数据在高位有序，低位也有序，所以最终整体有序
2.值得注意的是桶应该是一个先进先出的数据结构 3.数据必须有进制，才能使用基数排序

  
public class RadixSort {
  public static void radixSort(int[] arr){
    if (arr == null || arr.length < 2){
      return;
    }
    radixSort(arr, 0, arr.length-1, maxbits(arr));
  }
  public static int maxbits(int[] arr){
    int max = Integer.MIN_VALUE;
    for (int i = 0; i < arr.length; i++) {
      max = Math.max(max, arr[i]);
    }
    int res = 0;  // 计算最大数的位数
    while(max != 0){
      res++;
      max /= 10;
    }
    return res;
  }
  public static void radixSort(int[] arr, int L, int R, int digit){ //[L, R]，可以是局部排序也可以是整体排序
    final int radix = 10; //十进制是这个数
    int i = 0, j = 0;
    int[] bucket = new int[R - L + 1];  //准备与数组长度相同的辅助空间
    for (int d = 1; d <= digit; d++) {  //有多少位就进出几次（个位d=1，十位d=2，百位d=3）
      //10个空间
      // count[0] 当前位（d位）是0的数字有多少个
      // count[1] 当前位（d位）是1的数组有多少个
      // .....
      // count[i] 当前位是（0~i）的数字有多少个
      int[] count = new int[radix]; //count[0....9]
      for (i = L; i <= R; i++) {  //从左到右分析词频：在d位上相等的数据计数
        j = getDigit(arr[i], d);
        count[j]++;
      }
      for (i = 1; i < radix; i++) { //将词频分析完毕后的count数组处理：i下标的值等于i-1下标的值+自身，注意count数组初始化是数据均为0
        count[i] = count[i] + count[i - 1]; // 经过处理后的count[i]表示：d位上为i的数有多少个
      }
      for (i = R; i >= L; i--) {  //为什么是从R~L：为了继承上一次进桶出桶得到的排序，注意最初的数组顺序也是保留的
        j = getDigit(arr[i], d);
        bucket[count[j] - 1] = arr[i];  // 因为排序被继承，原先最右的，在第二次排序时也应该时同级别大小数据的最右，所以在辅助数组中的下标是count[j]-1，其中count[j]是同级别数据的个数，所以-1才是下标
        count[j]--;
      }
      for (i = L; i <= R; i++) {  //在将赋值数组的数据复制回原数组，这样一次进桶出桶完成
        arr[i] = bucket[i];
      }
    }

  }
  public static int getDigit(int x, int d){
    return ((x / ((int) Math.pow(10, d - 1))) % 10);
  }
}

详解桶排序及排序大总结

二叉树