介绍暴力递归

暴力递归 = 暴力 + 递归

对于递归，有下列规律：

递归函数要具体做什么（比如求1~10的和）
必须要有 basecase（即退出递归的条件）
必须缩小讨论的规模，求子问题，并且有得到了子问题之后的决策过程
不去深究递归过程是怎么样的，递归不记录子问题的解

对于暴力：

就是遍历所有的可能：关键在于如何列举出所有的可能

注意

何为规模缩小，即我们不从整体上（从头置为）去讨论一个问题，而是摘取其中一个部分进行讨论，比如对于一个序列 X[…i…]，我们优先讨论 i 和 i 之后的选择，i 之前的我们假设已经讨论过了

经典例题

汉诺塔问题

三个塔，把左边的 n 个圆盘按小的在上的规则移到右边的塔，问一共需要移动几步，并且打印这个过程

思路：

把所有 n 个圆盘看成一个整体，我们需要把 n 个圆盘从 from（左）移到 to（右）
为此我们首先要把上面 1~n-1 个圆盘移到 other（中间的塔），然后把 n 移到 to，再把 1~n-1 个盘移回从 other 移动到 to，重复 2 的操作

code 如下：

  
public class Solution{
    public static void hanoi(int n){
        if(n > 0){
            func(n, "左", "右", "中");
        }
    }

    public static void func(int i, String start, String end, String other){
        if(i == 1){
            System.out.println("Move 1 from" + start + " to " + end);
        }else{
            func(i - 1, start, other, end);
            System.out.println("Move " + i + " from" + start + " to " + end);
            func(i - 1, other, end, start);
        }
    }
    public static void main(String[] args){
        int n = 3;
        hanoi(n);
    }
}

leetcode 例题：面试题 08.06. 汉诺塔问题

  
public class Solution{
    /**
     * n：从 from 移到 to 的盘子数量
     * from：出发的塔
     * to：目标塔
     */
    public void hanota(int n, List<Integer> from, List<Integer> tmp, List<Integer> to){
        if(n <= 1){ //basecase
            Integer num = from.remove(from.size() - 1);
            to.add(num);
            return ;
        }
        hanoi(n-1, from, to, tmp);    //将盘子的上面 n-1 个一起从 from 移到 tmp
        Integer num = from.remove(from.size() - 1);   //然后把第 n 个盘子从 from 移到 to
        to.add(num);
        hanoi(n-1, tmp, from, to);    //再把那 n-1 个盘子一起从 tmp 移到 to
    }
}

打印字符串全部子序列，包括空字符串

什么叫做子序列

在数学中，某个序列的子序列是从最初序列通过去除某些元素但不破坏余下元素的相对位置（在前或在后）而形成的新序列。

后半句话的意思：子数列的次序必须和主数列的次序一样，另外序列自己也是自己的子序列

思路：

对于字符串上的每个字符，在子串中有两种情况：0-不存在，1-存在

解法1：

  
public class Solution1{
    public static void function(String str){
        char[] chs = str.toCharArray();
        process(chs, 0, new ArrayList<Character>());
    }
    public static void process(char[] str, int i, List<Character> res){
        if(i == str.length){
            printList(res);
            return;
        }
        //递归会自动回溯，我们关注的重点是不要让res是同一个引用，否则回溯的时候会出错
        List<Character> resKeep = copyList(res);
        resKeep.add(str[i]);
        process(str, i+1, resKeep); //保留当前字符
        process(str, i+1, res);    //不保留（可以直接传 res，而不用 copy，因为 res 的变化本身只依靠“保留这一操作”）
    }
    public static void printList(List<Character> res){
        for (Character ch : res) {
            System.out.print(ch);
        }
        System.out.println();
    }
    public static List<Character> copyList(List<Character> list){
        ArrayList<Character> chs = new ArrayList<>();
        list.forEach(chs::add);
        return chs;
    }
}

解法2（省空间）：

  
public class Solution2{
    public static void printAllSubsquence(String str){
        char[] chs = str.toCharArray();
        process(chs, 0);
    }

    public static void process(char[] str, int i){
        if(i == str.length){
            System.out.println(String.valueOf(str));
            return;
        }
        process(str, i+1);  //要当前字符
        char tmp = str[i];
        str[i] = 0;         //转义成空字符''
        process(str, i + 1);    //不要当前字符
        str[i] = tmp;         //回溯之前还原
    }
}

原题链接：打印全部子序列，题解如下：

  
public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 用来求出一个字符串的全部子序列，包含空字符串（因为这个不好统一输出的子序列，所以按照上课所讲写这个代码）
     * @param s string字符串 需要打印全部子序列的那个字符串
     * @return string字符串一维数组
     */
    public String[] getAllSubs (String s) {
        char[] chas = s.toCharArray();
        List<String> strList = new ArrayList<>();
        process(strList, chas, "", 0);
        String[] subs = strList.toArray(new String[0]);
        return subs;
    }
    private void process(List<String> strList, char[] chas, String curs, int i){
        if(i == chas.length){
            strList.add(curs);
            return;
        }
        //我并没有刻意去控制回溯，每次递归完之后，它自己就回溯了
        process(strList, chas, curs, i + 1);
        //这里每次连接字符串就成为了一个新的对象，必须每次是新的对象，否则一旦改变会影响到之前添加的旧的对象
        process(strList, chas, curs + chas[i], i + 1);
    }
}

打印一个字符串的全部排列（不出现重复的排列）

字符串的排列

思路：

不占任何空间，仅仅数组上交换位置生成不同的可能
如何生成不同的可能：数组上的每个位置都可由剩下的字符占用，还是以递归思路：假设 0…i-1 上的位置已经确定，i…n-1上的字符就有 i…n-1 上的字符交换生成
如何递归：如下图所示，先对数组上的位置遍历，然后对每个位置上可能的字符遍历
递归 basecase：当前遍历的位置 index = n - 1
如何去除重复：①如果字符的范围是 26 个大小写字母，可以使用一个 boolean 数组进行标记，如果范围更大就直接使用 HashSet 吧

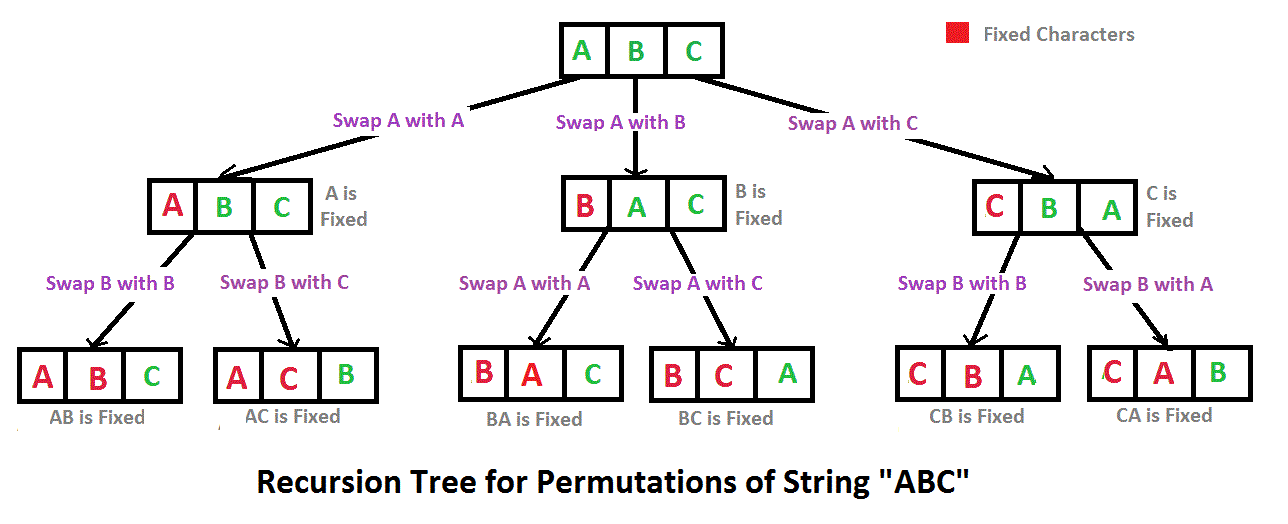
code：

  
public class Solution{
    public static List<String> permutation (String str) {
        // write code here
        List<String> res = new ArrayList<>();
        process(str.toCharArray(), 0, res);

        return res;
    }

    private static void process(char[] chs, int i, List<String> res){
        if(i == chs.length){
            res.add(String.valueOf(chs));
            return;
        }
        //如果字符的范围更广，那就改为 HashSet 结构吧
        boolean[] filter = new boolean[26];
        for(int j = i; j < chs.length; j++){
            int index = chs[j] - 'a' < 0 ? chs[j] - 'A' : chs[j] - 'a';
            if (!filter[index]){
                filter[index] = true;
                swap(chs, i, j);
                process(chs, i + 1, res);
                swap(chs, i, j);
            }
        }
    }
    private static void swap(char[] chs, int i, int j) {
        char tmp = chs[i];
        chs[i] = chs[j];
        chs[j] = tmp;
    }
}

拿纸牌问题

思路：

同样我们还是采用暴力递归的解法（老套路了，递归函数是干嘛的，basecase 是什么，如何决策并缩小规模成为子问题）

code 如下：

首先是定义我们的递归函数，简单梳理一下题意，玩家从任意一端取一张牌，最后的牌的数目之和最大谁就是赢家，并输出最大的和，其实对于这种为一个序列，求和或者是求最大值的题目最适合用暴力递归做了，题目中说玩家都绝顶聪明，即他们最后都会使得自己的分数最大化，由于先手又是固定的，所以我们的递归函数可以是这样：

  
/**
 * 在区间 [l, r] 上先手能获得的最大值
 */
private int f(int[] nums, int l, int r)

/**
 * 在区间 [l, r] 上后手能获得的最大值
 */
private int s(int[] nums, int l, int r)

注意：同一时刻先手和后手决策的区间一定是相同的，否者逻辑跑不通，或者说无法递归，即对于数组的某个区间 [l, r]，f 代表先手取得的最大值，s 代表后手取得的最大值，重申一遍：他们俩决策时的区间一定都是 [l, r]，而不是说先手是 [l, r]，后手就是 [l + 1, r] 或者 [l, r - 1]，理解了这一点，题目就完成了一半了（递归函数是干什么的讨论完成），接下来讨论该怎么决策：

先手和后手都递归一下
就递归先手，后手用总值减前者即可

这里只讨论第2点，第1点直接给出代码，也许你已经想到了，玩家1在取完第一轮牌后，相对于玩家2就是后手了，而后手必然被先手取得的结果影响，即区间 [l, r] 上的和的最小值，因为先手一定会取 [l, r] 上的和的最大值，理解了这一点离成功就只剩一步之遥了（决策过程讨论完成）

下面就是 basecase 了，很显然 l == r 就是 basecase，问题是我们该怎么退出，显然如果是先手，l == r 时，他就只能取这最后一张牌加到自己的和当中，如果是后手，l == r 就只能眼睁睁的看着先手取走了哈哈哈哈（basecase 讨论完成）

下面是 code：

  
/**
 * 第2点
 */
class Solution {
    public boolean PredictTheWinner(int[] nums) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }

        int fMax = f(nums, 0, nums.length - 1);
        return fMax > (sum - fMax) ? fMax : (sum - fMax);
    }

    private int f(int[] nums, int l, int r) {
        if (l == r){
            return nums[l];
        }
        return Math.max(nums[l] + s(nums, l+1, r), nums[r] + s(nums, l, r-1));
    }

    private int s(int[] nums, int l, int r) {
        if (l == r){
            return 0;
        }
        return Math.min(f(nums, l+1, r), f(nums, l, r - 1));
    }
}

  
/**
 * 第1点
 */
public class Solution{
    public static int win1(int[] arr){
        if(arr == null || arr.length == 0){
            return 0;
        }
        //返回先手和后手的最大值
        return Math.max(f(arr, 0, arr.length - 1), s(arr, 0, arr.length - 1));
    }
    //先手
    public static int f(int[] arr, int i, int j){
        if(i == j){
            return arr[i];
        }
        //先手完成一轮后，在下一轮变成后手
        return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
    }
    //后手
    public static int s(int[] arr, int i, int j){
        if(i == j){ //已经完成选牌，不需要后手了，所以直接返回0
            return 0;
        }
        //后手完成一轮后，在下一轮变成先手
        return Math.min(f(arr, i + 1, j), f(arr, i, j - 1));
    }
}

leetcode 相似题

486. 预测赢家

不申请额外的数据结构，只使用递归函数，逆序一个栈

即如何在只有一个栈的情况下，将栈内的数据逆序，这道题是非常典型的递归解法题，采用了经典的递归策略，从递归的老套路来书，思路永远是最简单的，我们只需要按照大脑的第一反映想到的解法辅以简单的递归套路就可完成，下面是思路和 code。

思路：

将栈底的元素出栈
逆序剩余其他元素的栈
将从栈底弹出的元素重新压栈

解析：通过第二点我们将问题缩小规模变成子问题，而整个解决方案的功能就是逆序一个栈

code：

  
import java.util.Stack;

public class Solution6 {
  /**
   * 反转栈
   * @param stack
   */
  public static void reverse(Stack<Integer> stack){
      //basecase
      if (stack.isEmpty()){
        return;
      }
      //弹出栈底的元素
      int item = getBottomItem(stack);
      //反转剩余其他元素的栈
      reverse(stack);
      //将栈底元素重新入栈
      stack.push(item);
  }

  private static int getBottomItem(Stack<Integer> stack) {
    Integer res = stack.pop();
    if (stack.isEmpty()){
      return res;
    }
    int i = getBottomItem(stack);
    stack.push(res);
    return i;
  }
}

数字转换字符串

思路：

这是典型的爬楼梯问题，这里可以爬一层，也可以爬两层，加上限制条件即可，感觉比较简单，所以直接上代码吧！

code ：

  
public class Solution{
  public static int translateNum(int num) {
    char[] arr = String.valueOf(num).toCharArray();
    return process(arr, 0);
  }

  private static int process(char[] arr, int i) {
    if (i >= arr.length - 1){
      return 1;
    }
    int count = 0;
    int num = Integer.parseInt(arr[i] + "");
    if (num == 1){
      return count + process(arr, i + 1) + process(arr, i + 2);
    }else if (num == 2){
      return Integer.parseInt(arr[i+1]+"") < 6 ? count + process(arr, i + 1) + process(arr, i + 2) : count + process(arr, i + 1);
    }else {
      //arr[i] = '0' || arr[i] >= '3'  
      return count + process(arr, i + 1);
    }
  }
}

原题链接：

剑指 Offer 46. 把数字翻译成字符串

0-1背包问题的贪心解法

code 如下：

  
public class Solution{
    //讨论 i 和 i 之后的货物选择，形成的最大价值返回
    //重量永远不要超过 bag
    //i 之前做的决定，所达到的重量，alreadyweight
    public static int process1(int[] weights, int[] values, int i, int alreadyweight, int bag){
        if(alreadyweight > bag){
            return 0;
        }
        return Math.max(
            process1(weights, values, i + 1, alreadyweight, bag), 
            values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag));
    }
}

详解暴力递归

介绍暴力递归

经典例题

汉诺塔问题

打印字符串全部子序列，包括空字符串

打印一个字符串的全部排列（不出现重复的排列）

拿纸牌问题

不申请额外的数据结构，只使用递归函数，逆序一个栈

数字转换字符串

0-1背包问题的贪心解法

相关文章

详解桶排序及排序大总结

HashMap遍历的三种方式

优先队列PriorityQueue