详解前缀树

介绍前缀树

何为前缀树

前缀树（Trie树），即字典树，又称单词查找树或键树，是一种树形结构，典型应用是用于统计和排序大量的字符串（但不限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的核心思想是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较。

如何创建前缀树 有如下字符串：【”abc”, “bck”, “abd”, “ace”】，建树过程如下：

1. 前缀树的根节点是空节点
2. 经典前缀树的字符都是在路径上的，而不是节点上
3. 对于每个字符，判断是否存在根节点到该字符的路径，没有就创建，有就复用
4. 虽然经典前缀树，节点上是没有额外信息的，但是为了某些功能，常常会把节点上的信息变得更加丰富

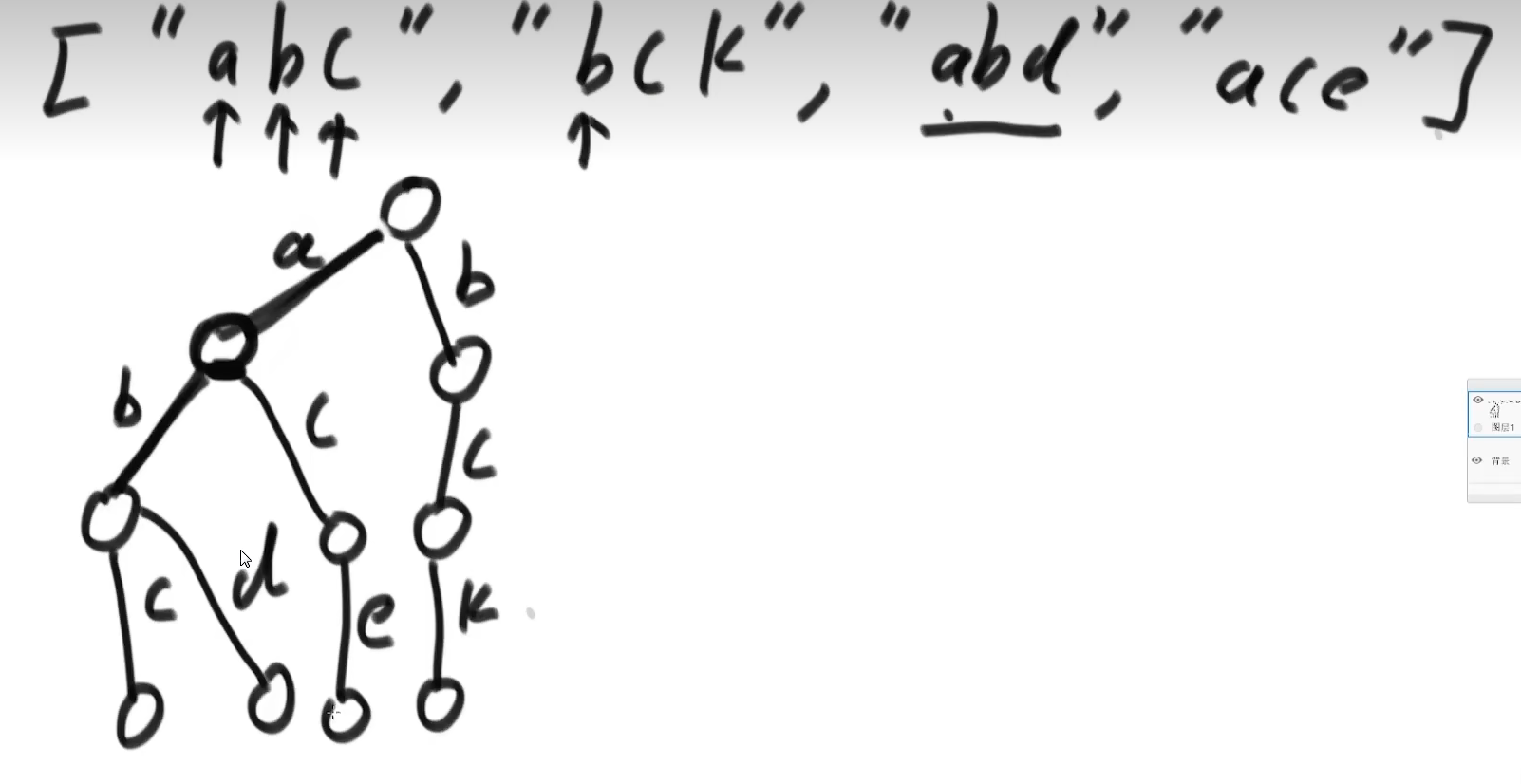
为节点添加丰富信息

前缀树节点code

public static class TrieNode{
  public int pass;
  public int end;
  //HashMap<Char, TrieNode> nexts
  //TreeMap<Char, TrieNode> nexts
  public TrieNode[] nexts;  //该节点下有无通向字符的路

  public TrieNode(){
    pass = 0;
    end = 0;
    //next[0] = null 没有走向‘a’的路
    //next[0] != null 有走向‘a’的路
    nexts = new TrieNode[26];   //我们定义了一个26容量的数组，0~25分别对应a~z
  }
}

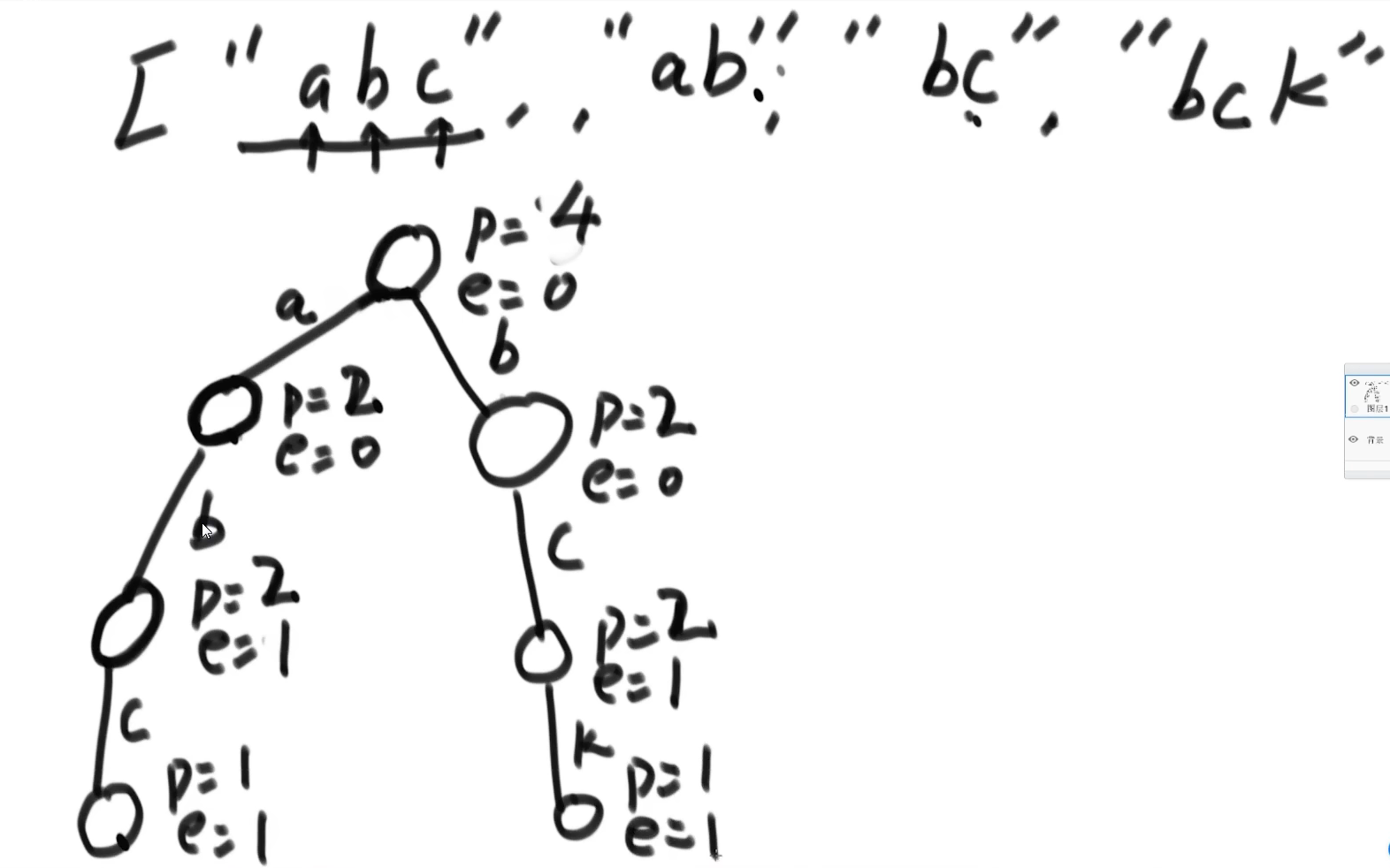
TrieNode中我们为节点丰富了更多的信息，如pass、end和nexts属性。 通过他们我们可以实现更多的功能：

1. pass 值：以根节点到该节点对应的字符串为前缀的字符串的数目，空节点的 pass 值表示以空串为前缀的字符串的数目
2. end 值是以根节点到该节点对应的字符串的数量
3. 通过 nexts，可知该节点下有没有路，如果nexts所有元素都为空那么就没有路了
4. 如果字符串的字符除了26个字母，还存在其他字符，那么可以使用 hash 表，如果需要每个节点下的路径是有序组织的，那么可以使用有序表结构

操作前缀树的方法

插入节点到前缀树

已知某字符在前缀树中不存在，就需要创建该字符对应的节点，code 如下：

public void insert(String word){
  if(word == null){
    return ;
  }
  char[] chs = word.toCharArray();
  TrieNode node = root;
  node.pass++;
  int index = 0;
  for(int i = 0; i < chs.length; i++){
    index = chs[i] - 'a'; //求路径在next中的下标
    if(node.nexts[index] == null){
      node.nexts[index] = new TrieNode();
    }
    node = node.nexts[index];
    node.pass++;    //这条路径有多少单词经过
  }
  //单词在前缀树中插入完成，当前节点是单词的尾节点
  node.end++;
}

解释一下节点的意思：节点即表示某条路径的终止，所以每条路径的最后都会存在一个节点，这也是为什么在插入业务中某个字符不存在我们是直接创建一个节点，创建了该节点就表示以该字符结尾的路径形成了或（子）字符串存入完毕了

查询某个单词在前缀树中加入过几次

code如下：

public int search(String word){
  if(word == null){
    return 0;
  }
  char[] chs = word.toCharArray();
  TrieNode node = root;
  int index = 0;
  for(int i = 0; i < chs.length; i++){
    index = chs[i] - 'a';
    if(node.nexts[index] == null){
      return 0; //如果字符串还未结束，路走不下去了，说明该字符串还未曾加入到前缀树
    }
    node = node.nexts[index];
  }
  return node.end;
}

所有加入的字符串中，有几个是以 pre 这个字符串作为前缀的

code如下：

public int search(String word){
  if(word == null){
    return 0;
  }
  char[] chs = word.toCharArray();
  TrieNode node = root;
  int index = 0;
  for(int i = 0; i < chs.length; i++){
    index = chs[i] - 'a';
    if(node.nexts[index] == null){
      return 0; //如果 pre 还未结束，路走不下去了，说明没有以 pre 作为前缀的字符串加入到前缀树中
    }
    node = node.nexts[index];
  }
  return node.pass;
}

删除某个单词在前缀树中的痕迹

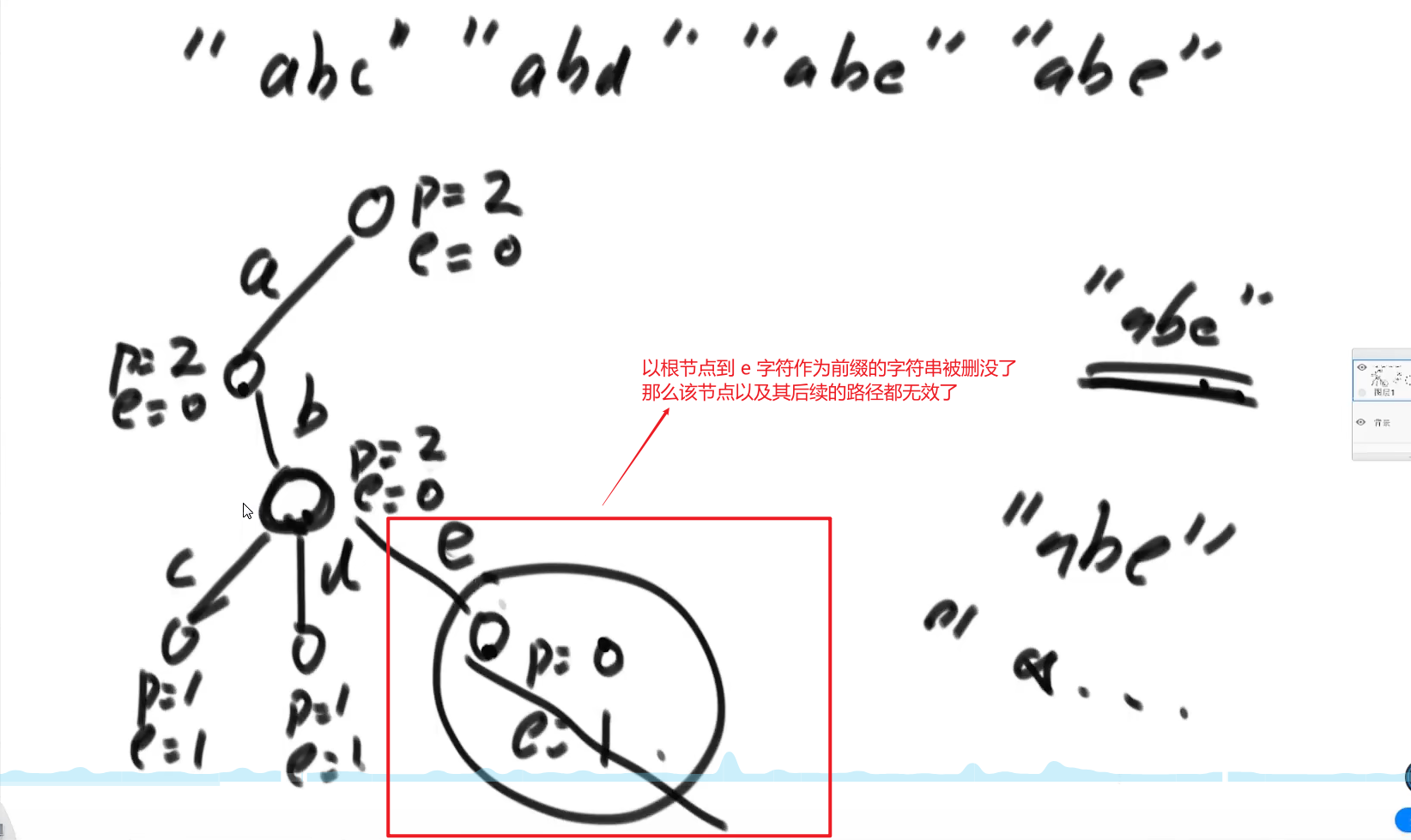
有两种情况：

1. 删除痕迹后，每个节点的 pass 都不为0
2. 删除后，存在某个节点的 pass == 0

code 如下：

public void delete(String word){
  if(search(word) != 0){  //首先得判断该字符串在前缀树种是否存在
    char[] chs = word.toCharArray();
    TrieNode node = root;
    node.pass--;
    int index = 0;
    for(int i = 0; i < chs.length; i++){
      index = chs[i] - 'a';
      if(--node.nexts[index].pass == 0){
        node.nexts[index] = null; //如果某节点对应的字符串，已经没有以它为前缀的了，后面的路径就都无效了，那么直接置为 null
        return;
      }
      node = node.nexts[index];
    }
    node.end--;
  }
}