认识O(NlogN)的排序

剖析递归行为和递归行为复杂度的估算

递归求数组最大值

  
public class RecursionArr {
  // right<arr.length，否则发送数组越界异常
  public static int process(int[] arr, int left, int right){
    if (left == right){
      return arr[left];
    }
    // (right-left)>>2 外面要加括号
    int mid = left + ((right-left)>>2);
    int num1 = process(arr, left, mid);
    int num2 = process(arr, mid+1, right);

    return Math.max(num1, num2);
  }
}

master公式

master公式是用来估算一类特殊的递归行为复杂度的方法，这类特殊的递归行为必须满足子问题规模相同才可使用master公式，公式如下：
T(N) = aT(N/b)+O(N^d)，其中a代表子问题调用的次数，N/b代表子问题规模，O(N^d)代表除子问题外的额外时间复杂度，如果满足master公式则有：
1.logb^a < d —> O(N^d)
2.logb^a > d —> O(N^{logb^a})
3.logb^a = d —> O(N^d·log^N)

使用master公式就可以很方便的估算一类递归行为的时间复杂度

归并排序O(NlogN)

  
public class MergeSort {
  public static void mergeSort(int[] arr){
    if (arr == null || arr.length < 2){
      return;
    }
    process(arr, 0, arr.length - 1);
  }

  private static void process(int[] arr, int L, int R) {
    if (L == R){
      return;
    }
    int mid = L + ( (R-L) >> 1 );
    process(arr, L, mid);
    process(arr, mid+1, R);
    merge(arr, L, mid, R);
  }

  private static void merge(int[] arr, int L, int M, int R) {
    int[] help = new int[R-L+1];
    int i = 0;
    int p1 = L;
    int p2 = M+1;
    while (p1 <= M && p2 <= R) {
      help[i++] = arr[p1] <= arr[p2] ? arr[p1++] : arr[p2++];
    }
    while (p1 <= M){
      help[i++] = arr[p1++];
    }
    while (p2 <= R) {
      help[i++] = arr[p2++];
    }
    for (i = 0; i<help.length; i++){
      arr[L+i] = help[i];
    }
  }
}

很显然归并排序满足master公式，求解可得：
①母问题规模即arr数组长度为N，子问题规模为N/2，b=2
②子问题被调用了2次，a=2
③额外复杂度即help填充值和help拷贝进原数组的过程，即2O(N)，那么就是O(N)，d=1
④logb^a = d
所以归并排序的时间复杂度是O(NlogN)

另外merge和process是在同一栈空间，而merge会引用辅助变量help，所以每次递归的空间复杂度是O(N)，调用完后就会销毁，所以最后的空间复杂度就是O(N)

小和问题

在一个数组中，每个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例子：
数组：[1, 3, 4, 2, 5] ，1左边比1小的数没有，3左边比3小的数，1，4左边比4小的数，1、3，2左边比2小的数，1，5左边比5小的数，1、3、4、2；所以小和为1+1+3+1+1+3+4+2=16

求解思路如下：
小和问题

按照归并的方法，数组每次会被分为左右两个区间，在merge的过程中，区间之间数据的绝对位置是没有改变的，也就是说对于左区间的某个数A来说，未二分之前和二分之后A都是在右区间的左边

merge在合并的过程中，如果左区间数据A小于有区间数据B，那么A会小于B和B右边的所有数据，因为两个区间本身是有序的

原题链接和我的题解

逆序对问题

在一个数组中，左边的数如果比右边的数大，则选择两个数构成一个逆序对，请打印所有的逆序对

分析思路同小和问题

原题链接

注意：
在该原题中：求余公式(a+b)%p=(a%p+b%p)%p

快速排序

快速排序1.0

荷兰国旗问题

问题1

给定一个数组arr，和一个数num，请把小于等于num的数放在数组的左边，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)
思路如下：
问题1

问题2（荷兰国旗问题）

给定一个数组arr，和一个数num，请把小于num的数放在数组的左边，等于num的数放在数组的中间，大于num的数放在数组的右边。要求额外空间复杂度O(1)，时间复杂度O(N)
颜色分类

该题解题思路比较多：

单指针，遍历两次数组，分别把nums[i]=0和nums[i]=1的交换到数组最左，其中第一次遍历0，指针最后的位置为p1，所以区间[0, p1-1]都是0，第二次遍历1，指针最后的位置是p2，所以区间[p1, p2]都是1，剩下的就都是2，这样数组就排好了。
因为数组的元素固定分别是0、1、2，所以统计出个元素的数量，然后按照左0，中1，右2的顺序放置元素，数组就排好了，需要两次遍历，第一次统计，第二次填充数组
双指针，如果双指针都从0开始，其中p0交换0，p1交换1，i负责遍历，需要注意得是：p0==p1时，p0每次交换，p1也要与p0同步+1，这步保证p1不会落后p0，但直到p0 < p1得时候，这个时候就不需要遵循先前得原则，因为p1 > p0，而如果现在p0需要交换，那么一定会把原本的1替换出去，这时需要由p1再次交换，然后两者都+1，也就是如果p1 > p0，后面就会一直大于
双指针，其中p0从0开始，p2从n-1开始，n=nums.length，p0负责交换0，p2负责交换2，i负责遍历

总结：不管怎么样第四种都是最右而且最简单得一种方法，所以还是优先采用第四种方式

快排2.0

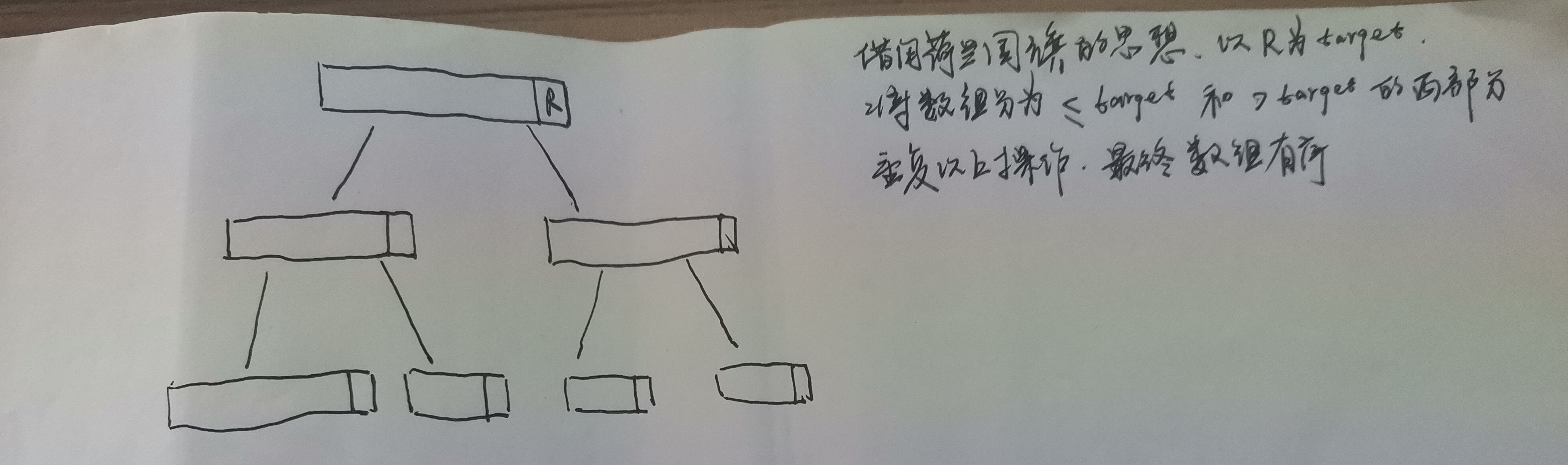
在划分分区时：将其分为三块，<target、==target和>target三部分，这样每次分区，所有==target的就被排序好了

快排3.0

快排1.0和快排2.0都有一个问题:
快排1.0和2.0存在的问题

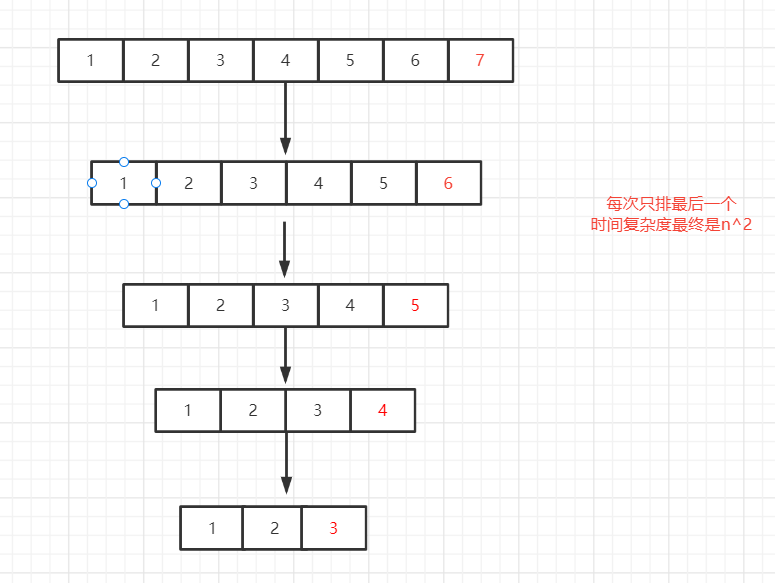
快排3.0为了不让target的选择过于固定，于是使用了生成随机位置的方法，最终在概率的加持下时间复杂度能保持在O(NlogN)
因为每次分层递归都需要额外的空间存储target，所以空间复杂度为O(logN)，

  
public class QuickSort {
  public static void quickSort(int[] arr){
    if (arr == null || arr.length == 0 || arr.length == 1){
      return;
    }
    quickSort(arr, 0, arr.length-1);
  }

  public static void quickSort(int[] arr, int L, int R){
    if (L >= R){
      return;
    }
    swap(arr, L + (int) (Math.random()*(R-L+1)), R);
    int[] p = partition(arr, L, R);
    quickSort(arr, L, p[0]-1);
    quickSort(arr, p[1]+1, R);

  }

  public static int[] partition(int[] arr, int L, int R){
    int less = L-1;
    int more = R;
    while(L < more){
      if (arr[L] < arr[R]){
        swap(arr, ++less, L++);
      }else if (arr[L] > arr[R]){
        swap(arr, --more, L);
      }else {
        L++;
      }
    }
    swap(arr, more, R);
    return new int[]{less+1, more};
  }

  public static void swap(int[] arr, int a, int b){
    int tmp = arr[a];
    arr[a] = arr[b];
    arr[b] = tmp;
  }
}