深入浅出索引

索引的实现模型

哈希表

模型结构如下：

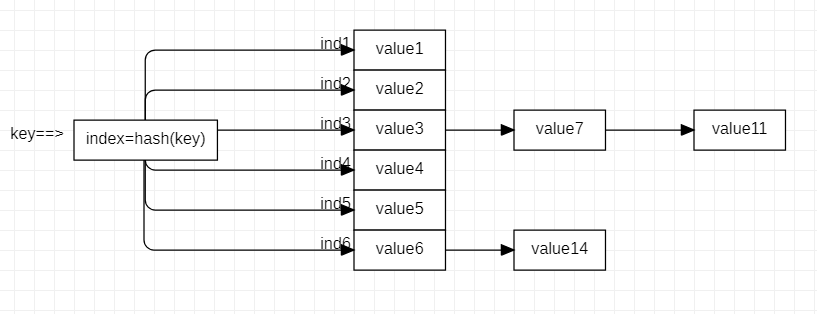
本哈希表以数组和链表为数据结构，哈希表通过哈希函数计算出索引可能的下标，并将值存在数组当中，如果不同的索引值命中相同的下标，那么会作为节点链接在数组元素后面；

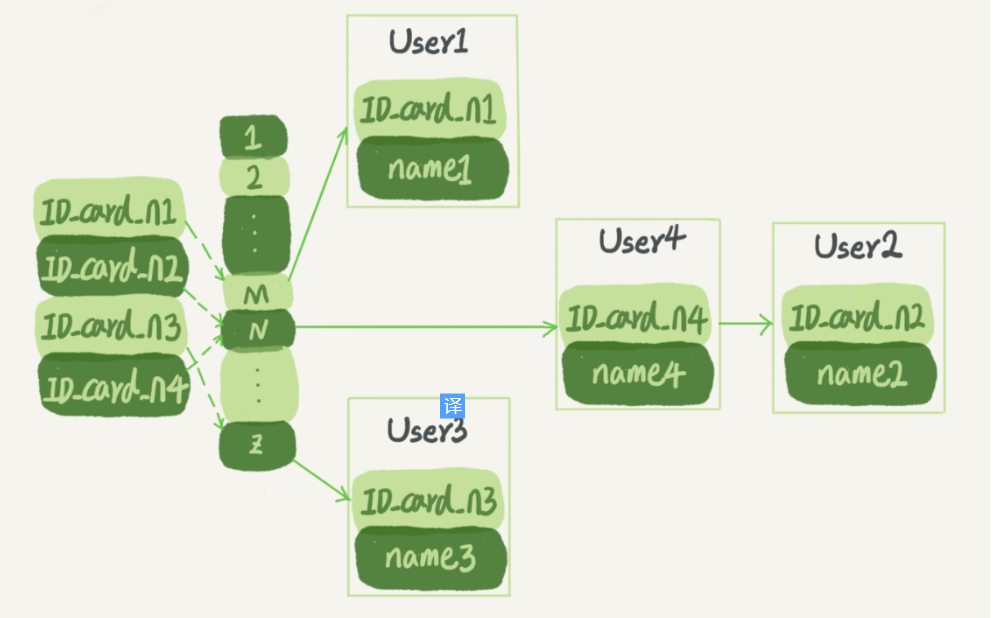
以Java的hashMap为例，数据以key-value键值对存在底层哈希表中，正如hashMap不会维护key值有序性，当我们针对一个区间查找数据的时候就会很麻烦，比如我的hashMap结构是一个Integer，User的键值对，存的是身份证id《—》居民信息由于数据存入时并没有保证有序性，当我们查找（101，201）这个区间的用户时，就要遍历所有的记录，直至查出所有的在这个区间的用户，所以说：哈希表这种结构适用于只有等值查询的场景，不适用范围查询，示意图如下：

有序数组

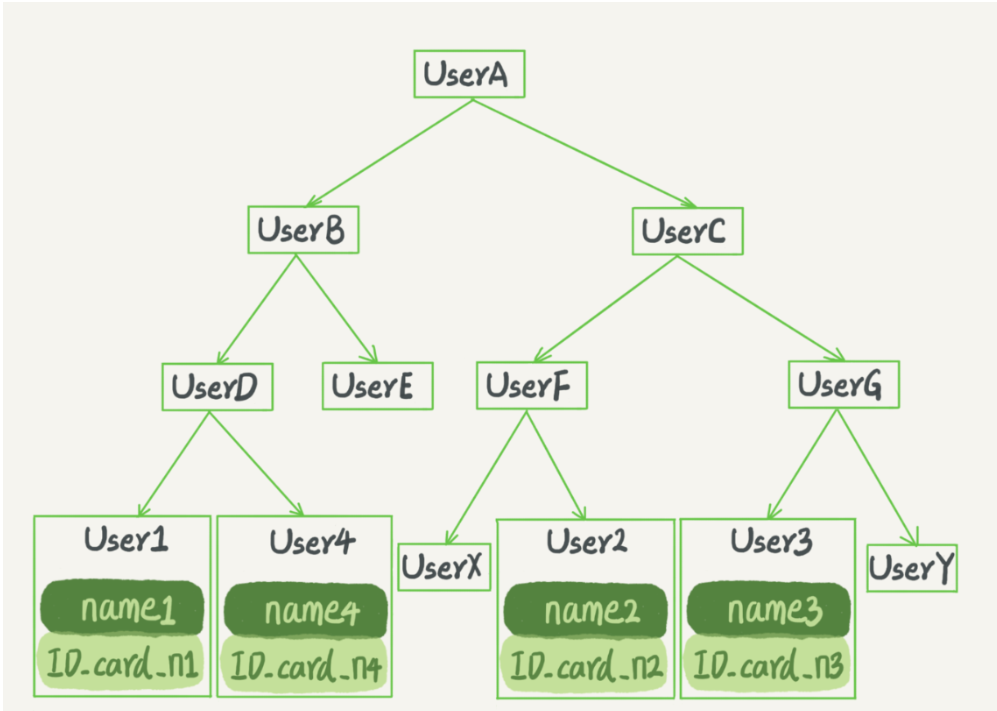
如果是有序数组，那么既可以保证身份证id的有序性，又能通过索引等值查询到需要的数据，这样看来有序数组完美适应等值查询和范围查询，但是如果向数组插入数据，就必须将后面的数据向后移动一段距离，时间复杂度可想而知，因此它适合静态数据的存储，如每年城市人口的数据

二叉搜索树

先来看看如果以身份证，用户信息作为案例：

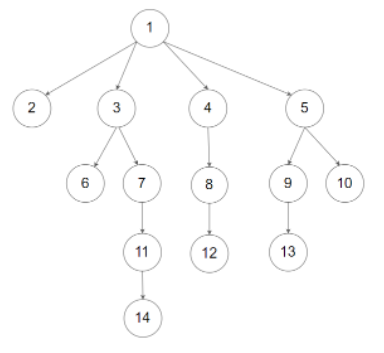
二叉树每个节点会分配一个权值，整好可以作为索引，为了保证二叉搜索树插入和查询的时间复杂度都是O(logn)，应该保证它是平衡二叉树（AVL树），二分查找树其实很像数组的二分查找，因而二叉树是一个查询效率很高的数据结构，不过它作为索引的底层数据结构却并不待见，原因是数据高度过高，每层固定是两个节点，那么对于一次搜索，很可能需要深入到树的底层，如果说每个节点存在磁盘，那么一次查找可能触发很多次IO操作，存储效率和查询效率都非常低

因而出现了多叉树，即尽量让一个数据块存更多的数据，这样就能有效降低树的高度，减少IO操作的次数，N叉树目前已经广泛应用于数据库引擎；

二叉树其实是特殊的N叉树，N叉树的基本结构和代码表示：

由于N叉树的根节点子数不确定，所以应该使用动态数组存储，在Java中我们就用ArrayList（当然实际上用的是接口List，毕竟LinkedList也不是不可以）

class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};

InnoDB的索引模型

InnoDB底层使用B+树作为索引的数据结构，B+树是更加复杂的多叉树，一个索引将会对应一棵B+树，索引—N叉树，1对1的关系；

B+树在数据库表上的表现：

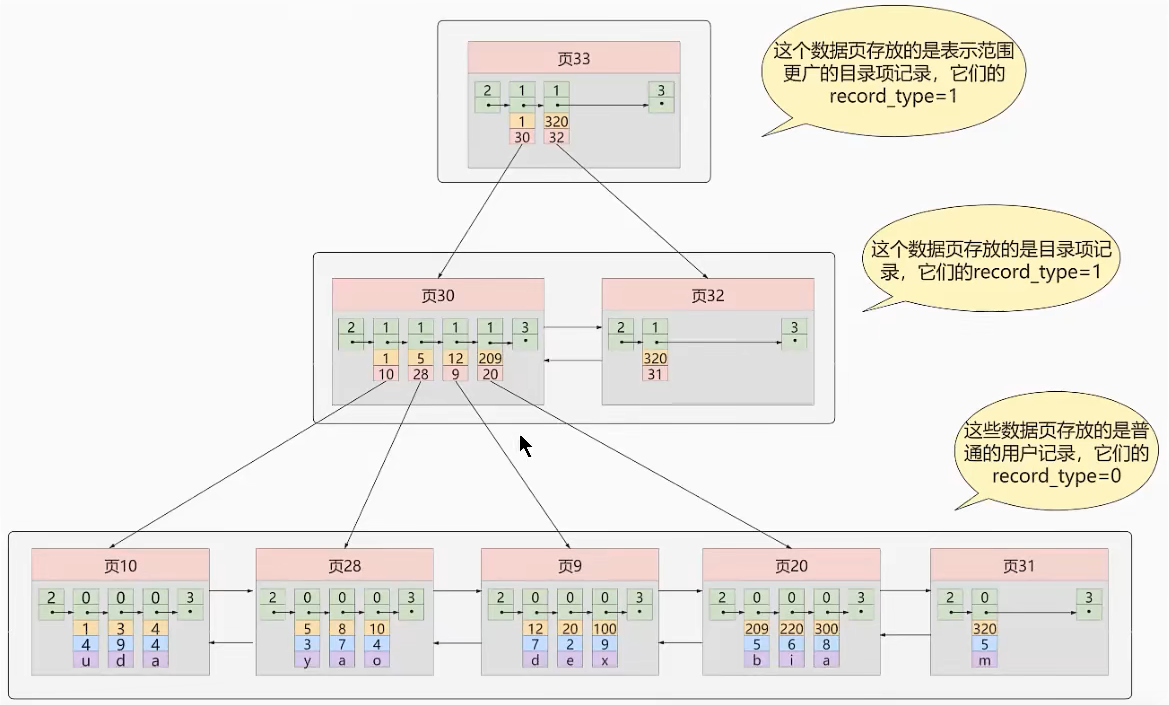
从图中可见，存储的数据类型有行记录，以及目录项，也就是索引，而叶子节点存储的都是行记录，非叶子节点也称为内节点

索引类型分为主键索引（聚簇索引）和非主键索引，主键索引叶子节点存的是一行的数据，而非主键索引存的是主键的值，因此，非主键索引也称为二级索引；显然使用非主键索引会多查一次树，因此主键索引的查询效率更高

索引维护

页分裂现象

下图是之前的身份证id-user的索引结构，以身份证Id作为索引：

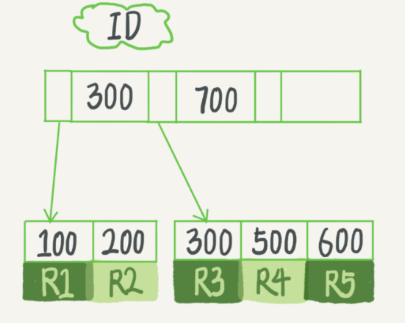
这个图该怎么看：ID下面的第一条数据实际是磁盘中连续的一段空间，而300与它后面的小的框框是一个整体，小的框框存的是一个数据页的地址，而300其实就是这个数据页的最小记录

为了保证索引的有序性，产生了所谓的页分裂，比如在R5之前插入数据，结果需要把R5的一部分数据往后挪，结果R5的数据分布在两个数据页，这就出现了页分裂

采用自增主键

在页分裂中我们看到，如果需要插入数据，B+树和有序数组一样，需要将后面的数据往后挪以腾出空间，但是如果是自增主键，每次只要追加就好了，因此推荐使用自增主键

自增主键和业务逻辑做主键

首先，主键长度越小，普通索引的叶子节点就越小，普通索引占用的空间也就越小。所以用自增主键是不错的选择；而业务逻辑主键不容易保存有序插入（比较可能比较复杂吧），这样写入操作可能耗时较多

什么时候适合用业务主键呢，K-V形式的场景，即：

1.整张表只有一个索引 2.索引必须是唯一索引

由于没有其他索引，就不用考虑主键占用空间较大的问题，对于插入问题，如果是整型还好，不是也没办法，毕竟有一个索引，相对而言使用索引查询和添加速率都会较快