时间复杂度
通常指最差情况下数据处理需要的开销,前提是数据量大的时候有效,原因是因为时间复杂度通常保存高阶,去掉低阶,如:
O(n2 +2n+c),通常表示为O(n2),显然在数据量小的时候不可能忽略后面的低阶的数据,但如果数据量足够大,就可以忽略后面的低阶了
常数操作
与数据量无关的操作,通常基本数据运算,如加、减、乘、除等属于常数操作
测试程序的优略
解决一个问题不同方法,我们往往通过时间复杂度判断优略,如果时间复杂度越小,性能就越好,但如果时间复杂度相同就应该实测判断,毕竟每个常数操作开销不同,如乘法大于加法的开销,加法大于位运算开销,因而用低阶部分判断优略是不合理的
空间复杂度
如果只需要借助几个变量,空间复杂度为O(1),如果额外的空间与程序使用的数据结构规模相当,那么就是O(n)
异或运算^
异或运算有种很便于记忆的性质,它可以看作无进位的加法
异或运算两数交换
通过异或运算可以快速的交换两个数:
1
2
3
4
int a=11,b=13;
a=a^b;
b=a^b;
a=a^b;
当然前提是a,b内存位置不一样,毕竟两个相同的数异或会清零
异或运算的性质
存在变量eor:
①0^eor=eor,②eor^eor=0,③满足交换律
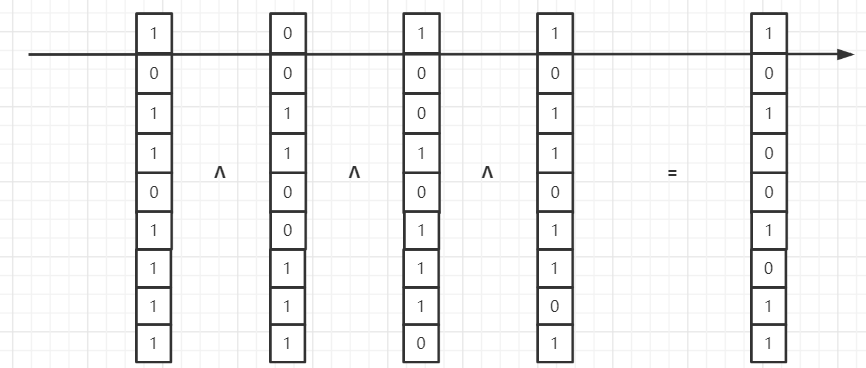
第三点证明:最终的结果取决于同一行上1的奇偶如果为奇,结果为1;如果为偶,结果为0;如下图
经典例题
1.存在数组,只有一类数出现奇数次,其余均出现偶数次,求这个出现奇数次的数 原题链接
2.有两种数存在奇数次,其余存在偶数次,求这个两种出现奇数次的数 原题链接
提示:假设两种数设为a,b,异或后的结果是eor;
由题意可得:a不等于b,即eor二进制上存在一位一定是1,且a,b在该位值一定不同,那么通过该为就可以将数据分为两类,一类是值=1,一类是值=2;
思路:
1.求eor最右为1的二进制数result,即如果eor=00010001,那么result=00000001。公式:result=eor&(~eor+1)或者result = eor & -eor
2.对数组分类:数组上的数与result做&运算,将等于0的一类统统异或,最终的结果就是a,或b中的一个,假设求出的值为x;
3.y=eor^x,其中x和y就是最终的结果
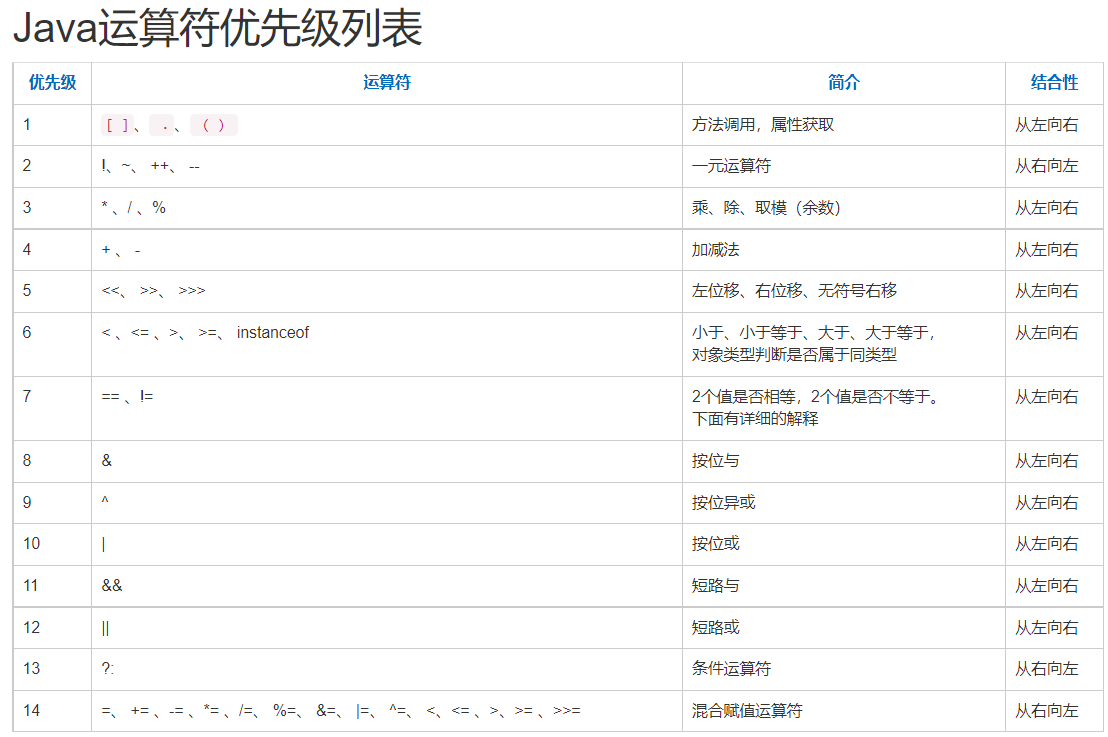
注意:& 和 == 的优先级顺序,实际上 == 的优先级大于 &,Java运算符优先级表如下:
选择排序O(N2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/**
* 选择出未排序的最小元素与排好序的末尾元素交换
*/
public class SelectionSort {
public static void doWork(Integer[] arr){
// 1.不合格的数组
if(arr==null || arr.length < 2){
return ;
}
// 2.arr.length-1个元素排好序后,整个数组就有序了
for (int i = 0; i < arr.length-1; i++) {
int minIndex = i;
// 3.在未排好序的数组中选择最小元素
for (int j = i+1; j < arr.length; j++) {
minIndex = arr[minIndex]>arr[j] ? j : minIndex;
}
// 4.交换
swap(arr, i, minIndex);
}
return ;
}
private static void swap(Integer[] arr, int x, int y){
Integer tmp = arr[x];
arr[x] = arr[y];
arr[y] = tmp;
}
}
冒泡排序O(N2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
* 冒泡排序,顾名思义泡泡从水底到水面逐渐变大
*/
public class BubbleSort {
public static void doWork(Integer[] arr){
// 0.不合格的数组
if (arr == null || arr.length < 2) {
return;
}
// 1.进行arr.length-1轮冒泡排序,能完成数组排序
for (int i = arr.length - 1; i > 0; i--) {
// 2.每轮需要完成的比较次数
for (int j = 0; j < i; j++) {
if (arr[j] > arr[j+1]) {
swap(arr, j, j+1);
}
}
}
}
private static void swap(Integer[] arr, int j, int i) {
Integer tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
}
插入排序O(N)~O(N2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/**
* 所谓插入排序,就是指对于有序的部分,插入一个数重排的过程
*/
public class InsertSort {
public static void doWork(Integer[] arr){
// 1.不合格的数组
if (arr == null || arr.length < 2) {
return;
}
// 2.要插入arr.length个数
for (int i = 0; i < arr.length; i++) {
// 3.首先保证当前插入元素所在的索引大于0,然后当前索引一定比前面的数小,才触发重排
for (int j = i; j > 0 && arr[j] < arr[j-1]; j--) {
swap(arr, j, j-1);
}
}
}
private static void swap(Integer[] arr, int j, int i) {
Integer tmp = arr[j];
arr[j] = arr[i];
arr[i] = tmp;
}
}
二分查找O(logN)
二分查找实例
1.在一个有序数组中,找某个数是否存在
2.在一个有序数组中,找>=某个数最左侧的位置
提示:
index变量记录到每次命中的元素下标,最小的index就是我们要的结果
3.局部最小:数组arr无序,任何两个相邻的数一定不相等,定义局部最小为: ①在0位置,如果arr(0) < arr(1),那么局部最小值在0位置;
②在n位置,如果arr(n) < arr(n-1),那么局部最小在n位置;
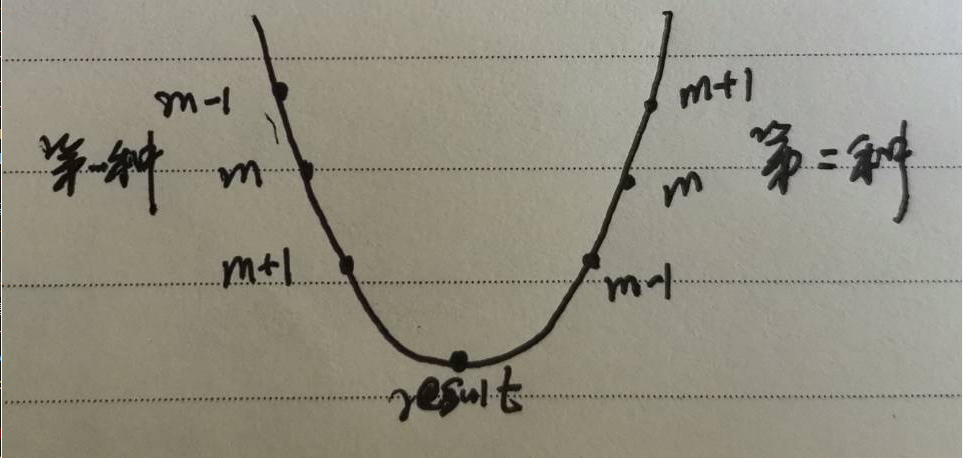
③对于中间位置m,如果arr(m) < arr(m-1),且arr(m) < arr(m+1),那么m是局部最小位置。
提示:①首先判断0和n位置;②二分法判断m-1,和m+1,此时可能出现两种情况:
第一种,m-1 > m > m+1,那么二分区间更新为(m+1,n)
第二种,m-1 < m < m+1,那么二分区间更新为(0,m-1)
局部最小相关题目:
寻找峰值 峰顶索引 山脉数组中查找目标值
对数器
- 有一个你想要测的方法a。
- 实现复杂度不好但是容易实现的方法b。
- 实现一个随机样本产生器。
- 把方法a和方法b跑相同的随机样本,看看得到的结果是否一样。
- 如果有一个随机样本使得比对结果不一致,打印样本进行人工干预,改对方法a或方法b。
- 当样本数量很多时比对测试依然正确,可以确定方法a基本正确。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
* 这是用来比较两个排序方法的正确性
* @param testTimes
* @param maxLength
* @param maxValue
*/
private void comparableDataMachine(int testTimes, int maxLength, int maxValue) {
// 1.循环测试testTimes次
for (int i = 0; i < testTimes; i++) {
// 2.生成随机长度的数组
int[] arr = new int[(int)(maxLength * Math.random())];
// 3.生成随机数组值
for (int j = 0; j < arr.length; j++) {
arr[j] = (int) (maxValue * Math.random());
}
// 4.拷贝新的数组
int[] copyArr = Arrays.copyOf(arr, arr.length);
// 5.分别对两对数组排序
BubbleSort.doWork(arr);
InsertSort.doWork(copyArr);
// 6.打印方法测试结果
if (Arrays.equals(arr, copyArr)) {
System.out.println("yes");
}else{
// 打印样本
System.out.println(arr.toString());
System.out.println("no");
}
}
}
