图的存储方式

如何表达图？生成图？图又分为无向图，有向图，它们该怎么表示

对于图G = (V，{E})，其中V表示顶点集合，E则是边的集合

邻接表

邻接表有下列两个结构：

顶点表
边表

结构如下：

邻接表结构

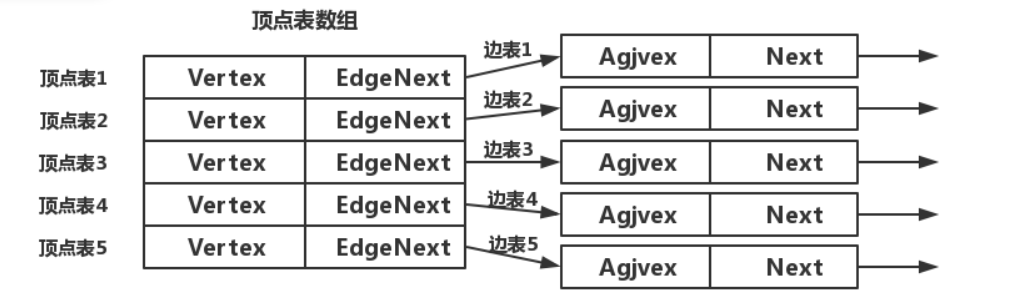
以无向图为例：

无向图无向图邻接表结构

参考：图的邻接表表示法（C语言）

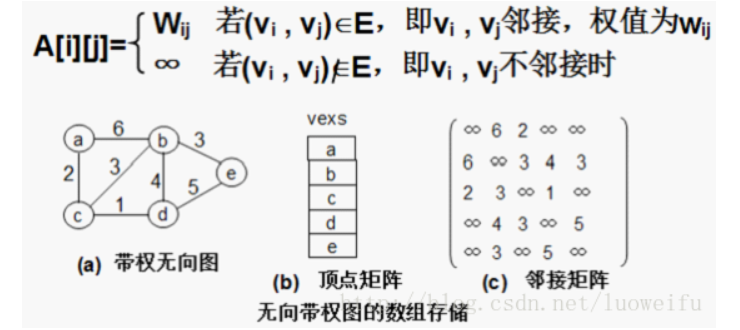
邻接矩阵

以无向图为例：

第一种是无向无权图的建模，无向无权图G=(V，E)有n(n≧1)个顶点，其邻接矩阵是n阶对称方阵，两顶点联通则为1，否则为0，其元素的定义如下：
第二种是无向有权图，这时矩阵值就是权值了，如果两顶点不连通则为正∞，建模如下：

参考：邻接矩阵表示法

统一图的表达

由于图的实现结构多种多样，对于每一种结构，都有一套不同的图运算api，因此要想掌握全部的图的表达方式非常困难，因此为了解题更加方便快速，我们应该选择自己喜欢和熟练的图的表达方式来实现所有的api，那么面对不同的结构，我们只需要将陌生的图结构转换成我们准备好的图结构就好了

我的图结构（邻接表）

图的总结构：即顶点集和边集

  
public class Graph{
  //顶点集：key是顶点的编号，value是顶点的实际结构，如果顶点结构较为简单，可以将哈希表替换为数组，这样效率会更高
  public HashMap<Integer, Node> nodes;
  //边集，Edge是边的结构
  public HashSet<Edge> edges;

  public Graph(){
    nodes = new HashMap<>();
    edges = new HashSet<>();
  }
}

顶点的实际结构Node

  
public class Node{
  //入度（无向图出度和入度相等）
  public int in;
  //出度
  public int out;
  //由当前顶点发散出去的边所连接的其他顶点（也被称为直接邻居）
  public ArrayList<Node> nexts;
  //当前顶点发散出去的边的集合
  public ArrayList<Edge> edges;

  public Node(int value){
    this.value = value;
    in = 0;
    out = 0;
    nexts = new ArrayList<>();
    edges = new ArrayList<>();
  }
}

边的实际结构Edge

  
public class Edge{
  //权值
  public int weight;
  public Node from;
  public Node to;

  public Edge(int weight, Node from, Node to){
    this.weight = weight;
    this.from = from;
    this.to = to;
  }
}

图的接口函数

  
public class GraphGenerator{
  /**
   * matrix是一个n*3的矩阵，其中n代表节点个数，这应该是个有向图
   * 结构：【weight, from节点上的值，to节点上面的值】
   */
  public static Graph createGraph(Integer[][] matrix){
    Graph graph = new Graph();
    for (int i = 0; i < matrix.length; i++) {
      Integer weight = matrix[i][0];
      Integer from = matrix[i][1];
      Integer to = matrix[i][2];
      //初始化图的顶点集，key为value，如果在图的顶点集中已经存在，就不需要存了
      if (!graph.nodes.containsKey(from)) {
        graph.nodes.put(from, new Node(from));
      }
      if(!graph.nodes.containsKey(to)){
        graph.nodes.put(to, new Node(to));
      }
      //初始化起点，终点，和边的实际结构
      Node fromNode = graph.nodes.get(from);
      Node toNode = graph.nodes.get(to);
      Edge newEdge = new Edge(weight, fromNode, toNode);
      //给起点添加直接领居
      fromNode.nexts.add(toNode);
      //出度++
      fromNode.out++;
      //终点的入度++
      toNode.in++;
      //添加到起点的发散的边集中
      fromNode.edges.add(newEdge);
      //添加到图的边集中
      graph.edges.add(newEdge);
      
    }
  }
}

图的宽度优先遍历

基本思路：

利用队列实现
从源节点开始依次按照宽度进队列，然后弹出
每弹出一个点，把该节点所有没有进过队列的邻接点放入队列
直到队列变空

code如下：

  
public class GraphGenerator{
  //从图的某个顶点出发
  public static void bfs(Node node){
    if(node == null){
      return;
    }
    Queue<Node> queue = new LinkedList<>();
    //相比于二叉树，图是可能存在环的，而set的作用就是为了避免遍历因为环陷入死循环，
    //我们将已经遍历的顶点记录在set中，这样就不会重复遍历了
    HashSet<Node> set = new HashSet<>();
    queue.add(Node);
    set.add(node);

    while(!queue.isEmpty()){
      Node cur = queue.poll();
      //如果是其他处理逻辑，就替换打印操作就行了
      System.out.println(cur.value);
      for (Node next : cur.nexts) {
        //如果顶点已存在set中，那么不对它重复处理，也就是不加到队列
        if(!set.contains(next)){
          set.add(next);
          queue.add(next);
        }
      }
    }
  }
}

图的广度优先遍历

基本思路：

利用栈实现
从源节点开始依次按照深度放入栈，然后弹出
每弹出一个点，把该节点下一个没有进过栈的邻接点放入栈
直到栈变空

code如下：

  
public class GraphGenerator{
  //从图的某个顶点出发
  public static void dfs(Node node){
    if(node == null){
      return;
    }
    Stack<Node> stack = new Stack<>();
    //相比于二叉树，图是可能存在环的，而set的作用就是为了避免遍历因为环陷入死循环，
    //我们将已经遍历的顶点记录在set中，这样就不会重复遍历了
    HashSet<Node> set = new HashSet<>();
    stack.add(Node);
    set.add(node);
    //如果是其他处理逻辑，就替换打印操作就行了
    System.out.println(cur.value); 
    //最后栈的弹出顺序就是深搜路径   
    while(!stack.isEmpty()){
      Node cur = stack.pop();

      for (Node next : cur.nexts) {
        //如果顶点已存在set中，说明已经在深搜路径当中了，我们应该找还没走过的路
        if(!set.contains(next)){
          //先逮住一个直接邻居，一路走到黑，同时会把当前节点重新压入栈中，因为该入口可以还有其他路需要探索
          stack.push(cur);
          stack.push(next);
          set.add(next);
          System.out.println(next.value);
          //深搜路径继续延申，这是我们来到了新的路口，所以退出上一个路口的循环
          break;
        }
      }
    }
  }
}

拓扑排序

适用范围：要求有向图，且有入度为0的节点，且没有环（没有循环依赖，假设存在循环依赖，那么可能压根就没有入度为0的节点，这样也就求不出拓扑排序）
适用场景：依赖的编译顺序，即依赖A需要先编译，因为编译依赖B的时候需要依赖A，这时的顺寻就是A -> B

算法步骤：

找到入度为0的节点，放入队列
从队列中弹出节点，放到顺序数组中，将这个节点的直接邻居的入度-1，相当于把这个节点和它发散出去的边从图中消除
重复1，2操作，直到队列为空，返回顺序数组

code如下：

  
public class GraphGenerator{
  public static List<Node> sortedTopology(Graph graph){
    //hash表记录每个节点当前的入度，key为节点node，value为入度，value会随着入度为0的节点及其发散边的消除而变化
    HashMap<Node, Integer> inMap = new HashMap<>();
    //只有入度为0的时候才会放到这个队列
    Queue<Node> zeroInQueue = new LinkedList<>();
    //1.初始化inMap
    //2.并且找到第一批的入度为0的节点（注意入度为0的节点可以一次性会有多个）
    for (Node node : graph.nodes.values()) {
      inMap.put(node, node.in);
      if(node.in == 0){
        zeroInQueue.add(node);
      }
      
    }
    //顺序数组
    List<Node> result = new ArrayList<>();
    while(!zeroInQueue.isEmpty()){
      Node cur = zeroInQueue.poll();
      result.add(cur);
      //将入度为0的节点的影响消除，并且找出下一批的入度为0的节点
      for (Node node : cur.nexts) {
        //将邻居节点的入度-1
        inMap.put(next, inMap.get(next)-1);
        if(inMap.get(next) == 0){
          zeroInQueue.add(next);
        }
      }
    }

    return result;
  }
}

最小生成树

请思考一个问题：假设要在n个城市之间建立通信联络网，则联通n个城市只需要n-1条线路，那么如何在最省经费的前提下建立这个通信网？因为n个城市之间，最多可能设置n(n-1)/2条线路，那么如何在这些可能的线路中选择n-1条，使得总的耗费最少呢？生成最小生成树

下面将介绍两种解决【构造连通网的最小代价生成树】问题的方法：

Prim算法
Kruskal算法

Kruskal

基本思路：首先假设对于非连通图T = (V, {}),此时只有顶点集，没有边，现在依次将代价最小的边加入，如果加入的边在在图中会形成环，那么这条边就不加了，遍历所有的边执行上述相同的操作，最后生成的图就是最小生成树

如果判断是否会形成环

首先假设对于非连通图T = (V, {})，每个顶点自成一个连通分量，若代价最小的边的依附的顶点分别在不同的连通分量中，就加入T中，否则不加入，加入之后，该连通分量就是这两个顶点的集合

总结步骤如下：

最初每个顶点自成一个连通分量（初始化工作）
准备一个依照边的权值从小到大的排序集合（例如小根堆，每次弹出的就是最小代价的边）
依次加入代价最小的边，如果边E依附的顶点A和B在不同的连通分量就加入到T中，并且将两个连通分量合并成一个，即将{A}与{B}合并成{A,B}，那么原来的连通分量{A}，{B}就不存在了（合并操作）
重复上诉操作，直到遍历了所有的边（循环遍历操作）

补充： 1.连通图：任意两个节点之间都有一条联通的路径，则是连通图，否则叫做非连通图
2.连通分量：即极大连通子图，如下图【连通分量】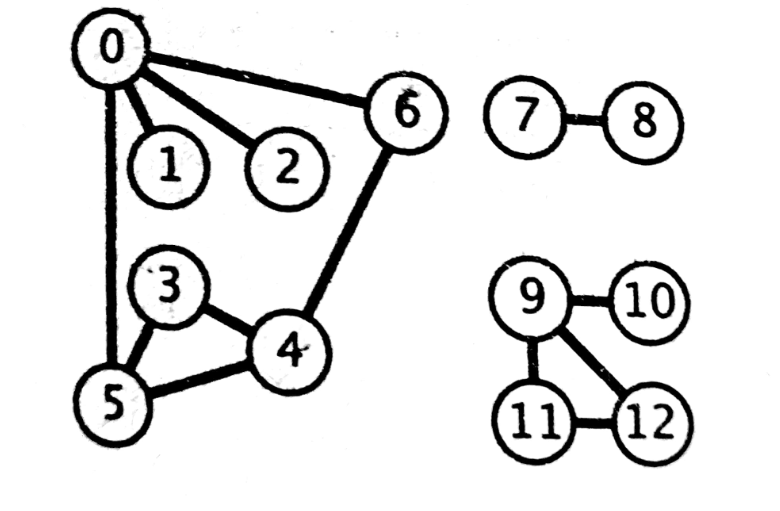

在该图片中，图G由三个部分组成，{0,1,2,3,4,5,6}，{7,8}，{9,10,11,12}，而这三个部分就是图G的三个连通分量

code如下：

  
public class Kruskal{
  //每个顶点对应的连通分量
  private HashMap<Node, List<Node>> setMap;
  private Kruskal(){
    setMap = new HashMap<>()
  }
  /**
   * 初始化连通分量，起初每个顶点自成一个连通分量
   */
  public void makeSets(List<Node> nodes){
    for (Node cur : nodes) {
      List<Node> set = new ArrayList<Node>();
      set.add(cur);
      setMap.put(cur, set);
    }
  }
  
  /**
   * 判断边两个顶点是否在同一个连通分量中
   */
  public boolean isSameSet(Node from, Node to){
    List<Node> fromSet = setMap.get(from);
    List<Node> toSet = setMap.get(to);
    //两个集合不是同一个集合，即同一个连通分量
    return fromSet == toSet;
  }

  /**
   * 将边的两个顶点所属的不同的连通分量合并在一起
   */
  public void union(Node from, Node to){
    List<Node> fromSet = setMap.get(from);
    List<Node> toSet = setMap.get(to);
    //将其中一个连通分量的顶点合并到另一个连通分量中，并更新setMap
    for (Node toNode : toSet) {
      fromSet.add(toNode);
      setMap.put(toNode, fromSet);
    }
  }

  public static Set<Edge> kruskalMST(Graph graph){
    Kruskal kruskal = new Kruskal();
    //初始化连通分量
    kruskal.makeSets(graph.nodes.values());
    PriorityQueue<Edge> pq = new PriorityQueue<>(new Comparator<Edge>(){
        public int compare(Edge o1, Edge o2) {
          return o1.weight - o2.weight;
        }
        
    });
    //准备好最小代价的边的排序集合
    for (Edge edge : graph.edges) {
      pq.add(edge);
    }
    Set<Edge> result = new HashSet<>();
    while(!pq.isEmpty()){//遍历每条边
      Edge edge = pq.poll();
      if(!kruskal.isSameSet(edge.from, edge.to)){
        result.add(edge);
        kruskal.union(edge.from, edge.to);
      }
    }
    return result;
  }
}

Prim

基本思路：首先对于图N = (V, {E})，任意选择一个顶点作为起始连通分量U，我们从U = {u0}(u0 ε V),TE = {}开始，其中TE是最小生成树边的集合，重复进行下面的操作：在所有的u ε U，v ε V-U 的边(u, v) ε E中找到一条代价最小的边(u0,v0)添加到TE中，并将v0并入到连通分量U中，直到U = V为止，此时T = (U, {TE})就是MST。

Prim算法和Kruskal算法的关系

其实Prim的思路和kruskal的思路是一样的，都是在不同的连通分量通过最小代价的边进行融合，最后形成MST，在kruskal中是不同的连通分量随机融合，而Prim算法中，融合的连通分量一方是固定的，即U，另一方就是V-U，V-U是剩余顶点（也就是连通分量的集合）

Code如下：

  
public class Prim{
  public static Set<Edge> primMST(Graph graph){
    PriorityQueue<Edge> pq = new PriorityQueue<>(new Comparator<Edge>(){
        public int compare(Edge o1, Edge o2) {
          return o1.weight - o2.weight;
        }
    });
    //初始连通分量
    HashSet<Node> uSet = new HashSet<>();
    //MST的边的集合
    Set<Edge> teSet = new HashSet<>();

    for (Node node : graph.nodes.values()) {//这个遍历保证V中的所有顶底最终都会合并到uSet中
      if(!uSet.contains(node)){//第一个随机的初始点形成最初的连通分量
        uSet.add(node);
        for (Edge edge : node.edges) {//把所有的边存入pq，注意这里会有重复的边，也就是边的两个顶点都在uSet中的，但是不慌后面的if条件会筛掉
          pq.add(edge);
        }
        while(!pq.isEmpty()){
          Edge edge = pq.poll();  //弹出连通分量的所有顶点发散的边中的最小边
          Node toNode = edge.to;
          if(!uSet.contains(toNode)){//筛掉重复的边（边的两个顶点都在uSet中）
            set.add(toNode);          //合并V-U中的顶点
            teSet.add(edges);       //将最小代价边添加到MST的边集合中
            for (Edge nextEdge : toNode.edges) {
              pq.add(nextEdge);
            }
          }
        }
      }
    }
  }
}

从代码量来看Prim算法完胜，但相对kruskal要更加难理解写

总结

Kruskal和Prim算法针对的都是无向图的最小生成树（MST）算法

单源最短路径

这个算法就是求某个源点到其他各顶点的最小距离，因此这种算法必须决定一个源点，下面介绍解决该问题的算法：

Dijkstra算法

Dijkstra

基本思路：

选一个源点A，初始化源点到其他顶点的距离（包括源点自己）序列，此时到其他源点的距离为正无穷，到源点自己的距离是0
从最短距离序列中，找出到源点距离最小的顶点B，用该顶点去更新其他顶点到源点的距离（包括他自己），即假设更新的顶点是C，原本A -> C，距离是10，而A -> B距离是2，B -> C距离是5，所以A -> B -> C距离是7，比原本距离短，就更新，否则不更新。选到的点后面就不再选了，比如B这一轮更新完后，下一轮就不再选它
重复2的操作，直到所有顶点都被选过

注意：Dijkstra 没有负数的边，所以它是不支持负值的，并且不能存在环（从后面的代码中看：在计算最小距离的时候负值和环都是不允许存在的，否在会导致程序错误）

code如下：

  
public class Dijkstra{

  /**
   * head就是选择的源点
   */
  public static HashMap<Node, Integer> dijkstra(Node head){
    HashMap<Node, Integer> distanceMap = new HashMap<>(); //代表node到head的距离n，value就是n
    //初始时，只有head到自己的距离，并且value=0，其他未添加的表示距离为正无穷
    distanceMap.put(head, 0)
    //存放已经选过的顶点
    HashSet<Node> selectedNodes = new HashSet<>();
    //获取距离到head最小的顶点，并用它更新其他顶点到head的距离
    Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);

    //当所有顶点都被选过后，停止循环
    while(minNode != null){
      int distance = distanceMap.get(minNode);
      for (Edge edge : minNode.edges) {
        Node toNode = edge.to;
        //如果顶点到head的初始距离为正无穷，则直接更新
        if(!distanceMap.containsKey(toNode)){
          distanceMap.put(toNode, distance + edge.weight);
        }
        //否则将原来的距离与更新后的距离比较，留下最小的
        distanceMap.put(toNode, Math.min(distanceMap.get(toNode), distance + edge.weight));
      }
      //一轮更新完成，将minNode打入到selectedNodes
      selectedNodes.add(minNode);
      minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNodes);
    }
    return distanceMap;
  }

  public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap, HashSet<Node> touchedNodes){
    Node minNode = null;
    int minDistance = Integer.MAX_VALUE;
    //遍历所有顶点，找出没有选过并且距离最小的顶点
    for (Entry<Node, Integer> entry : distanceMap.entrySet()) {
      Node node = entry.getKey();
      int distance = entry.getValue();
      if(!touchedNodes.contains(node) && distance < minDistance){
        minNode = node;
        minDistance = distance;
      }
      
    }
    return minNode;
  }
}

Dijkstra的堆加速算法

思路：

未优化时从 distanceMap 中选取一个最小并且没有被用过的 Node 是采用 for 循环遍历的方式，而为了加速算法我们可以通过小根堆优化这个步骤：

起初将所有数据放入小根堆，每次弹出一个值，用于更新其他 Node 到 head 的距离
在堆中更新值，有需要保持小根堆的结构系统自带的实现是做不到的，因此我们需要手写堆，并对这种更新操作进行实现

code 如下：

  
public class Solution{
  /**
  * 从 head 出发，所有 head 能到达的节点，生成到达每个节点的最小路径记录并返回
  * size：总共的节点数
  * 返回值：每个 Node 到 head 的最短距离
  */
  public static HashMap<Node, Integer> dijkstra2(Node head, int size){
    NodeHeap nodeHeap = new NodeHeap(size);
    /**
      * addOrUpdateOrIgnore 方法
      * add --> 每添加一条新的记录
      * update --> 记录已存在，并且 Node 到 head 的距离更短，就更新
      * ignore --> 记录已存在，但更新的距离要大，就忽略
      */
    nodeHeap.addOrUpdateOrIgnore(head, 0);
    HashMap<Node, Integer> result = new HashMap<>();
    while(!nodeHeap.isEmpty()){
      //每弹出一个 Node，更新它的直接节点
      NodeRecord record = nodeHeap.pop();
      Node cur = record.node;
      int distance = record.distance;
      for(Edge edge : cur.edges){
        /**
          * edge.to：直接节点
          * edge.weight：到直接节点的距离
          * distance：cur 到 head 的距离
          */
        nodeHeap.addOrUpdateOrIgnore(edge.to, edge.weight + distance);
      }
      result.put(cur, distance);
    }
    return result;
  }
  public static class NodeRecord{
    public Node node;
    public int distance;
    public NodeRecord(Node node, int distance){
      this.node = node;
      this.distance = distance;
    }
  }
  public static class NodeHeap{
    private Node[] nodes; //所有的节点放在 nodes 数组当中
    private HashMap<Node, Integer> heapIndexMap;  //堆中的 node 在数组中的 index，当 index == -1，表示 node 已经被选择过了
    private HashMap<Node, Integer> distanceMap;
    private int size;
    public NodeHeap(int size){
      nodes = new Node[size];
      heapIndexMap = new HashMap<>();
      distanceMap = new HashMap<>();
      size = 0;
    }
    public boolean isEmpty(){
      return size == 0;
    }
    public void addOrUpdateOrIgnore(Node node, int distance){
      if(inHeap(node)){
        distanceMap.put(node, Math.min(distanceMap.get(node), distance));
        insertHeapify(node, heapIndexMap.get(node));
      }
      //从没进入过堆的，增加记录
      if(!isEntered(node)){
        nodes[size] = node;
        heapIndexMap.put(node, size);
        distanceMap.put(node, distance);
        insertHeapify(node, size++);
      }
    }
    public NodeRecord pop(){
      NodeRecord nodeRecord = new NodeRecord(node[0], distanceMap.get(nodes[0]));
      swap(0, size - 1);
      heapIndexMap.put(nodes[size - 1], -1);
      distanceMap.remove(nodes[size - 1]);
      nodes[size - 1] = null;
      heapify(0, --size);
      return nodeRecord;
    }
    //有问题
    private void insertHeapify(Node node, int index){
      while(distanceMap.get(nodes[index]) < distanceMap.get(nodes[(index - 1) / 2])){
        swap(index, (index - 1) / 2);
        index = (index - 1) / 2;
      }
    }
    //有问题
    private void heapify(int index, int size){
      int left = index * 2 + 1;
      while(left < size){
        int smallest = left + 1 < size && distanceMap.get(nodes[left + 1]) < distance ? left + 1 : left;
        smallest = distanceMap.get(nodes[smallest]) < distanceMap.get(nodes[index]);
        if(smallest == index){
          break;
        }
        swap(smallest, index);
        index = smallest;
        left = index * 2 + 1;
      }
    }
    private boolean isEntered(Node node){
      return heapIndexMap.containsKey(node);
    }
    private boolean inHeap(Node node){
      return isEntered(node) && heapIndexMap.get(node) != -1;
    }
    private void swap(int index1, int index2){
      heapIndexMap.put(nodes[index1], index2);
      heapIndexMap.put(nodes[index2], index1);
      Node tmp = nodes[index1];
      nodes[index1] = nodes[index2];
      nodes[index2] = tmp;
    }

  }


}

图

图的存储方式

邻接表

邻接矩阵

统一图的表达

我的图结构（邻接表）

图的宽度优先遍历

图的广度优先遍历

拓扑排序

最小生成树

Kruskal

Prim

总结

单源最短路径

Dijkstra

相关文章

详解桶排序及排序大总结

HashMap遍历的三种方式

优先队列PriorityQueue